Einstieg in die Laufdatenanalyse
Ein Lauf mit der Garmin Fenix 3 Laufuhr produziert schon für kleine Laufeinheiten eine relativ große Datenmenge die im Garmin *.fit Format auf der Uhr abgespeichert wird. In der Regel hat der User seine Laufuhr mit dem Handy gekoppelt oder überträgt per WLAN diese Daten an sein zuvor eingerichtetes Garmin-Connect Konto. Sind die Daten übertragen kann, man sich dazu Auswertungen in seinem Konto anschauen. Der Pace-Graph sieht in Garmin Connect dann z.B. so aus:
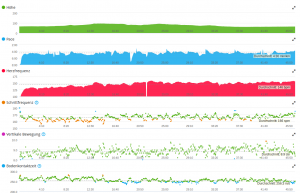
Hier sticht im ersten Moment der sehr „volatile“ Verlauf der Zeitreihe ins Auge. Da der Autor selber diese Strecke gelaufen ist, kann er die „spikes“ mit z.B. 3:07 min/km sicher ausschließen d.h. dies sind ausschließlich GPS-Messfehler. Diese spikes haben unangenehme Eigenschaften:
- Das Minimum und Maximum der Zeitreihe besteht i.d.R nur aus Messfehlern.
- Liegt ein spike in einem kurzen Laufsegment, wird der Mittelwert stark verzerrt.
- Die spikes verstellen den Blick aufs Ganze da man kaum Trends, die Wirkung von Anstiegen etc. ausmachen kann.
- Die Skalierung der Ordinate fällt durch die spikes ungünstig aus.
Daneben gibt es noch eine weitere Sicht in Garmin Connect auf den Lauf.
- die Skalierung der Achsen ist nicht immer befriedigend
- Die Wahl des Zeichenmodus – gefüllte Fläche, Linie Punkte – ist vorgegeben
- Die Daten können nur über Zeit oder Distanz auf der Abszisse gezeichnet werden. Insbesondere wird jede andere multivariate Betrachtung nicht unterstützt.
Zusammenfassend kann man für die Grafiken festhalten:
- Lokal kommt es zu großen Verzerrungen im Tempo
- Die Sicht auf die Laufdaten ist vielfach unbefriedigend
- Ein kausaler Zusammenhang zwischen Tempo und den anderen Messgrößen kann grafisch kaum abgeleitet werden. Das sind aber die Größen, an denen der Läufer arbeiten kann, um seine Pace zu verbessern.
Das ganze Prozedere von Lauf bis abschließender Analyse wirft die Frage auf, wer Eigentümer und Besitzer der Daten ist. Für viele Läufer dürfte der Besitz d.h. die Verfügung über das Eigentum sehr eingeschränkt sein. Man hat eigentlich nur eine voreingestellte Sicht auf die Daten, kann aber nicht mit ihnen arbeiten. Der Autor hat bis jetzt noch kein frei zugängliches Tool wie z.B. gps-babel gefunden, dass sämtliche Felder des Fenix3 fit-file ausließt. Deshalb wurde hier der „harte“ Weg beschritten, der aber Programmierkenntnisse voraussetzt. Dazu beschafft man sich ein Garmin SDK, spielt dieses in eine Entwicklungsumgebung ein und erstellt sich per Programm die nötigen Dateien aus dem fit Format. Diese kann man dann z.B. mit GNU R auswerten.
Die Zeitreihe Tempo zu diesem Lauf weißt folgende Autokorrelationen auf:
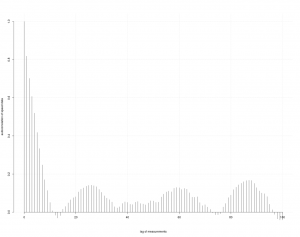
Es zeigt sich also ein signifikanter positiver Zusammenhang für die ersten ca. 10 Lags, der auch zu erwarten war. Danach ist kein signifikanter Einfluss mehr erkennbar. Als Einstieg in die multivariate Datenanalyse bietet sich häufig ein Scatterplot an.
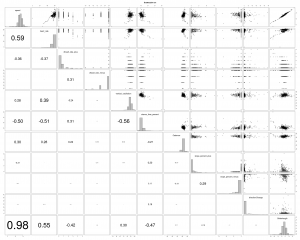
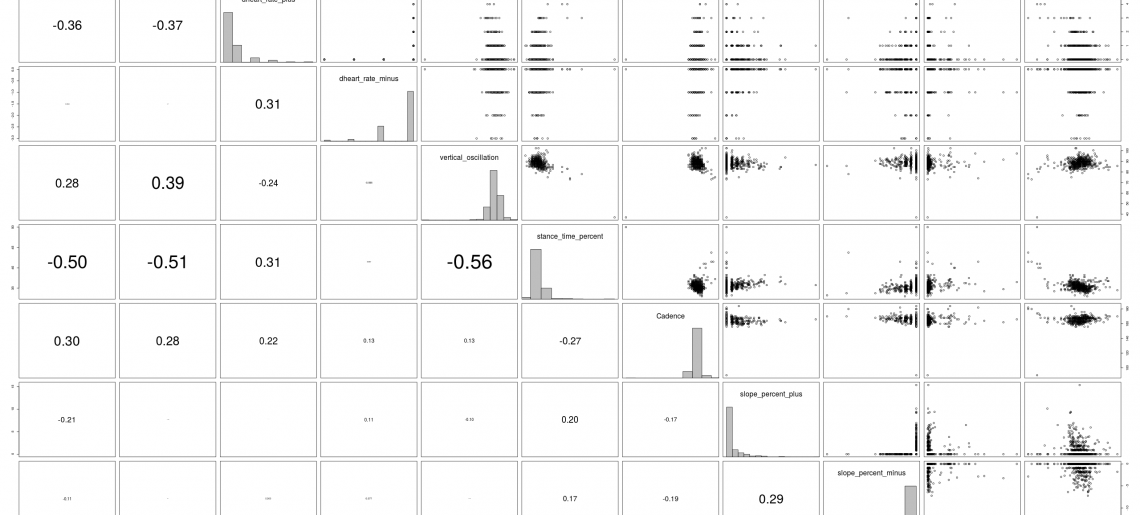
Auf der Hauptdiagonalen befinden sich die Histogramme zu den Variablen, im oberen Dreieck die Scatterplots und im unteren Dreieck die Korrelationen. Uns interessiert hier zunächst der Zusammenhang zwischen Speed und den anderen Variablen. Im Scatterplot sind das die erste Zeile und erste Spalte. Demnach ist der Zusammenhang zwischen Speed und (stride length, heart rate, stance time %) am stärksten und mit dem fachlich erwarteten Vorzeichen ausgeprägt.
- stride length: Die Schrittlänge wird bei Garmin über Schrittfrequenz und zurückgelegten Weg ermittelt. Sie ist deshalb mit den selben Fehlern des GPS Signals behaftet aus denen die Geschwindigkeit ermittelt wird. Die hohe Korrelation könnte auf diesem Fehler-Zusammenhang beruhen.
- heart rate wird über den Brustgurt gemessen. Ist dieser am Anfang des Laufs nicht feucht, kann es zu größeren Fehlen kommen. Der Autor hält deshalb den Brustgurt vorher kurz unter warmes Wasser.
- stance time % wird über die Erschütterung gemessen. Je länger man auf dem Boden bleibt, desto schlechter die Pace.
Für diese Daten wird nun folgendes linear homogene Modell (d.h. ohne Konstante) in R angesetzt:
lm(formula = speed ~ 0 + time + time2 + heart_rate + heart_rate_lag1 + heart_rate2 + vertical_climb_plus + vertical_climb_minus + Cadence + stance_time_percent + vertical_oscillation, data = rundata, weights = w)
Um den spikes entgegen zu wirken wird ein IRLS (vgl. https://en.wikipedia.org/wiki/Iteratively_reweighted_least_squares) Ansatz mit reziproken Gewichten zur Nachbildung der L1-Norm gewählt.
| Independent Variable | Estimate | Std. Error | t value | Pr(>|t|) | signif |
| time | -1,38E-003 | 1,85E-004 | -7,438 | 4,12E-013 | *** |
| time2 | 3,43E-007 | 5,40E-008 | 6,346 | 4,74E-010 | *** |
| heart_rate | 1,80E-001 | 1,93E-002 | 9,332 | < 2e-16 | *** |
| heart_rate_lag1 | -1,03E-002 | 2,57E-003 | -3,985 | 7,69E-005 | *** |
| heart_rate2 | -3,14E-004 | 7,81E-005 | -4,018 | 6,70E-005 | *** |
| vertical_climb_plus | -1,20E-003 | 1,36E-004 | -8,777 | < 2e-16 | *** |
| vertical_climb_minus | -2,38E-004 | 1,13E-004 | -2,111 | 0,0352 | * |
| cadence | 4,66E-002 | 6,62E-003 | 7,048 | 5,66E-012 | *** |
| stance_time_percent | -3,13E-001 | 2,87E-002 | -10,924 | < 2e-16 | *** |
| vertical_oscillation | -2,20E-003 | 7,89E-003 | -0,278 | 0,7808 |
und eine hochsignifikante Regression:
Residual standard error: 0.855 on 532 degrees of freedom
Multiple R-squared: 0.9984, Adjusted R-squared: 0.9984
F-statistic: 3.345e+04 on 10 and 532 DF, p-value: < 2.2e-16
Die Zeit geht mit 2 Termen (time, time2=time*time) ein. Hier wird eine nach oben offene Parabel im Wertebereich [-1.4; -0.2] km/h geschätzt mit Minimum auf dem letzten Drittel des Laufs. Die Herzfrequenz geht mit 3 Termen ein (heart_rate, heart_rate2, heart_rate_lag1). Bezüglich des quadratischen Teils (heart_rate, heart_rate2) zeigt sich ein erwartungsgemäß degressiver Verlauf d.h. abnehmender Grenznutzen des sich „quälen“. Die Variable heart_rate_lag1 hat ein negatives Vorzeichen d.h. je niedriger die Herzfrequenz in der Vorperiode desto höher die aktuelle Geschwindigkeit. Die Variablen zum Anstieg gemessen in Höhenmeter/Zeit haben das erwartete Vorzeichen. Hier fällt auf, dass der Tempoverlust beim Anstieg größer ausfällt als der Tempogewinn bei „downhill“ bzw. dieser nur mäßig signifikant ist . Eine Erklärung hierfür könnte sein, dass man sich beim Bergablauf ausruht. Die Schrittfrequenz hat erwartungsgemäß einen positiven Einfluss aufs Tempo. Die Verweildauer auf dem Boden hat erwartungsgemäß einen negativen Einfluss aufs Tempo. Die Hebung des Oberkörpers (vertical_oscillation) hat hier einen negativen, aber nicht signifikanten Einfluss. Das Vorzeichen entspricht hier der fachlichen Theorie, aber wahrscheinlich ist dieser Zusammenhang eher über eine Querschnittsstudie – Vergleich mehrer Läufer – und über längere Distanzen nachweisbar. Die Gegenüberstellung von Rohdaten und Modellprognose führt zu folgender Grafik: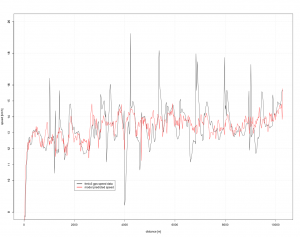
Die Modellprognose verläuft hier schon deutlich ruhiger und realistischer. Die spikes sind erfolgreich eliminiert worden.
