Die Leistung – gemessen in Watt – ist im Radsport eine zentrale Größe und kann selbst im Freizeitbereich mit Messgeräten zu erschwinglichen Preisen zuverlässig ±4% bestimmt werden. Diese messen die sogenannte äußere Leistung die auf Pedal, Kurbel oder Nabe wirkt und somit direkt geschwindigkeitswirksam ist. Der Athlet hat damit in „real time“ ein Leistungsfeedback.
Im Laufsport ist die Leistung aber bisher dem Freizeitläufer kaum zugänglich. Die Zweckmäßigkeit eines Laktattest zur Einstufung der Leistungsfähigkeit von Freizeitsportlern wird selbst vom DFB vor dem Kostenhintergrund bezweifelt. Daneben sind dies keine Echtzeit-Informationen und können so im konkreten Lauf kaum helfen.

Ein ähnliche Funktion wie die Echtzeit-Leistungsmessung im Radsport hat die Herzfrequenz im Laufsport, die mit Brustgurt oder mittlerweile auch mit optischen Sensoren am Handgelenk gemessen wird. Diese dürfte statistisch gesehen sehr hoch mit der Leistung korreliert sein.

Meine Erfahrungen aus dem Radsport gehen dahin, dass ein Watt-Messgerät ganz erheblich die Leistung steigern und objektivieren kann. Während die Herzfrequenz gefühlt eher das „sich quälen„ misst, ist die Leistung ein zuverlässiges Maß, an dem man sich orientieren kann. Unter widrigen Umständen – Steigung, Gegenwind, schlechter Untergrund, viele Kreuzungen – ist man ohne Wattmeter häufig unzufrieden mit der eigenen Leistung, obwohl kein Anlass dazu besteht. Unter günstigen Umständen ist es anders herum. Man gibt sich zufrieden, obwohl noch viel mehr möglich ist.

Daneben ist es aus Sicht des Autors schon fast pathologisch, die Laufleistung mit dem „sich quälen“ abzuschätzen. Das Ziel sollte doch eher darin bestehen, eine Laufleistung mit möglichst wenig Schmerz zu erbringen. Vermutlich führt dieses „sich quälen“ Paradigma gepaart mit Ehrgeiz bei unerfahrenen Läufern zu den Sportverletzungen an Fuß, Knie und Bein.

Das Problem ist aber, dass man die Leistung im Laufsport in der Regel nicht vorliegen hat. Deshalb soll im Folgenden die Leistung aus den Datenfeldern einer Laufuhr abgeleitet werden. Der hier verfolgte Ansatz orientiert sich an den Gleichungen von Dr. Lälles erklärt’s . Dieser Ansatz baut im wesentlichen auf der Veränderung der potentiellen Energie d.h. der Lageenergie bei einem Laufschritt auf.

$\begin{array}{lcl} % P(t)_{\mbox{\small Hubleistung}} & = & m_{\mbox{\small Läufer}} g H(t) \,\, K(t) \\ P(t)_{\mbox{\small Beinbeschleunigung}} & = & c K(t) \\ P(t)_{\mbox{\small Luftwiderstand}} & = & \frac{1}{2} r_{\mbox{\small Luft}} A_{\mbox{\small Läufer}} c_{w \,\mbox{\small Läufer}} v(t)_{\mbox{\small Läufer}}^3\\ P(t)_{\mbox{\small netto}} & = & P(t)_{\mbox{\small Hubleistung}} + P(t)_{\mbox{\small Beinbeschleunigung}} + P(t)_{\mbox{\small Luftwiderstand}}\\ P(t)_{\mbox{\small brutto}} & = & \frac{1}{\eta} P(t)_{\mbox{\small netto}} + P(t)_{\mbox{\small Grundumsatz}}\\ W_{\mbox{\small Lauf}} & = & \sum_i t_i P(t_i)_{\mbox{\small brutto}} \\ \hline \multicolumn{3}{l}{ \mbox{\small mit: } t= \mbox{\small Zeit}, H(t)=\mbox{\small vertikal Hub}, K(t)=\mbox{\small Kadenz}, v(t) =\mbox{\small Geschwindigkeit}, W_{\ldots} = \mbox{\small Arbeit}, P_{\ldots} = \mbox{\small Leistung}}\\ \multicolumn{3}{l}{ \mbox{\small und Parametern: } m=70,\quad g =9.81,\quad c=10,\quad r A c_w/2= 0.2889378414\quad \eta=0.21 } \end{array} %$

Zeit, Vertikal Hub, Kadenz und Geschwindigkeit werden von der Laufuhr gemessen. Hier muss aber beachtet werden, dass diese Daten mit Fehlern und Ausreißern behaftet sind.
Die anderen Konstanten sind der Literatur – insbesondere Dr. Lälles erklärt’s entnommen – sowie geringfügig modifiziert worden um zu vergleichbaren Ergebnissen bei der Gesamtkalorienmenge W(Lauf) zu kommen. Insbesondere ist die Gleichung für Beinbeschleunigung angepasst worden. Widerstandskräfte wie isometrische Arbeit und Reibung in den Gelenken sind hier nicht explizit berücksichtigt und schlagen sich so im Wirkungsgrad η nieder.
Gegen- oder Rückenwind sind nicht abgebildet.
Ebenfalls sind Auf- und Anstiege nicht modelliert. Hier würde sich zudem die Frage stellen, ob die Anstiege zu einem gewissen Teil schon im Vertikalhub enthalten sind.
Die Nettoleistung ist die äußere Leistung die für die Bewegung nötig ist. Die Bruttoleistung ist die Leistung die der Körper erbringen muss. Dazwischen liegen Grundumsatz und Wirkungsgrad η.
Bei allen Variablen ist auf die Verwendung von SI – Einheiten zu achten (m/s, 1/s) bzw. entsprechend umzurechnen.
Da hier nur die Grundrechenarten in überschaulicher Anzahl verwendet werden, spricht nichts dagegen dies in Echtzeit in einer Laufuhr auszuführen und anzuzeigen. Bei der Garmin Fenix 3 ist dies derzeit aber nicht vorgesehen.

Die Nettoleistung steht damit in Abhängigkeit von $P(t)_{\mbox{\small netto}} & = & c_1 H(t) K(t) + c_2 K(t) + c_3 v(t)^3$

wobei fürs Freizeitlaufen aus dem ersten Term mehr als 80% der Leistung kommen dürfte. Demnach würde ein um 1% gesteigerter Hub und eine um 1% gesenkte Kadenz ungefähr zur gleichen Leistung führen. Das mag physikalisch erklärbar sein, für den Läufer dürfte dies aber nicht ratsam sein. Man sollte im Gegenteil bei konstanter Leistung eher die Kadenz erhöhen und den vertikal Hub senken. Dies wird deutlich, wenn man zusätzlich die Schrittweite S betrachtet. Bei konstanter Schrittweite würde die erste Variante mit gesenkter Kadenz nämlich auch zu einer 1% niedrigeren Geschwindigkeit führen. Der Bezug des Vertikalhubs zur Geschwindigkeit ist eindrucksvoll in folgender Grafik dargestellt.

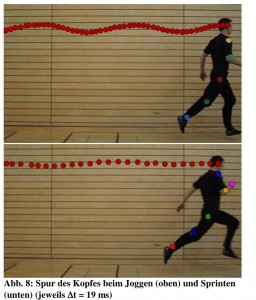
Quelle: Weidt, M. und T. Wilhelm (2015) Gehen und Laufen im Physikunterricht, S. 8

Man sieht in der Abbildung deutlich, dass hier beim Joggen der Kopf – und mit ihm der Schwerpunkt – deutlich stärker vertikal ausgelenkt wird als beim Sprint.

Nimmt man die Gleichung für die Hubleistung und nutzt den Zusammenhang zwischen Geschwindigkeit, Kadenz und Schrittweite nach $v(t) = S(t) K(t)$ so ergibt sich, da $S > 0, \quad P_{\mbox{\small Hub}} = m g \frac{H}{S} v$ . Bei konstanter Hubleistung, Hub und Schrittweite führt eine um 1% gesteigerte Masse zu einer Geschwindigkeitssenkung von ebenfalls 1%. Leichte Läufer sind hier also im Vorteil, und so etwas ähnliches besingen auch „Silbermond“ mit

Du nimmst all den Ballast
und schmeisst ihn weg,
Denn es reist sich besser,
mit leichtem Gepäck.

Der Läufer sollte also möglichst lange Beine für den Schritt und möglichst wenig Masse haben. Da aber die Körperlänge sowohl mit Beinlänge als auch Masse positiv korreliert seien dürfte – zumindest bei Leichtathleten, behäbige Wohlstandsbürger ausgeklammert – liegt das Optimum irgendwo in der Mitte und Arne Gabius (derzeit 1.86m, 66kg) dürfte schon Aufgrund der Größe eher am rechten Rand der Verteilung bei Topläufern liegen.
Für eine möglichst schnelle und energetisch günstige Bewegung kann man das folgende Problem betrachten:

$\begin{eqnarray*} \max\limits_{S,H,K} (v-P_{\mbox{\small Hubleistung}}) &=& S K -c_1 H K \\ & = & S(K - c_1 K {H/S}) = SK(1-c_1 \tan(\phi)) \\ & = & v (1-c_1 \tan(\phi)) \end{eqnarray*}$

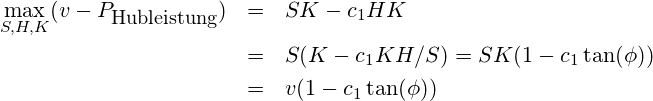
Die optimale Lösung hätte demnach maximale Geschwindigkeit (an der oberen Grenze des Möglichen) bei minimalen Winkel ϕ an der unteren Grenze.

Aber was hat man sich hier unter der Winkel ϕ vorzustellen? Formal ergibt er sich aus dem Verhältnis Hub zu Schrittweite. Eine damit positiv korrelierte Größe dürfte der Absprungwinkel sein. Das ist der Winkel, mit dem der Fuß den Boden verlässt. Und diesen kann der Läufer durch den „Laufstil“ beeinflussen. Mit

$P_{\mbox{\small Hubleistung}}= m\, g\, v\, tan(\phi)$

haben wir also eine instruktive Schreibweise für die Hubleistung gefunden. Dieser Fragestellung soll in einer weiteren Analyse nachgegangen werden. Insbesondere hängt hier die Leistung linear von der Geschwindigkeit $v$ ab. Diese Funktionsform findet man auch in der Literatur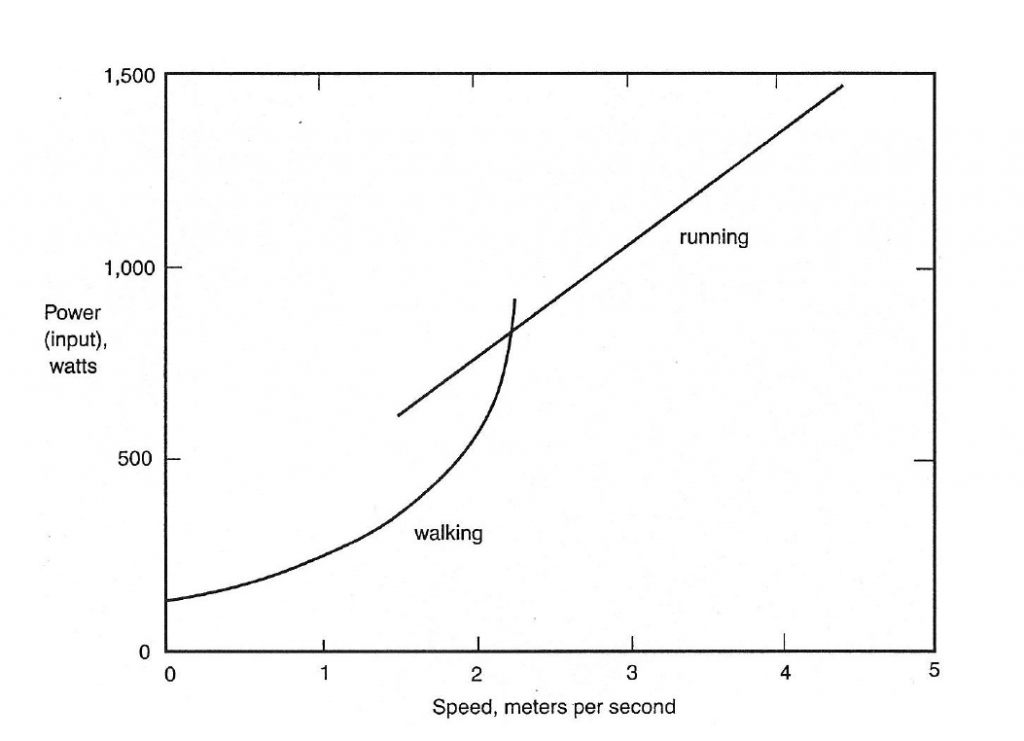

Quelle: Waller, D. (2008), S.17

Leistung und Geschwindigkeit

Diese Gleichungen zur Leistung werden nun auf eine Trainingslaufaufzeichnung von Sportplatzrunden angewendet.

Die GPS Aufzeichnung deckt sich ganz gut mit dem Sportplatz und Ausreißer in Längen- und Breitengrad sind nicht erkennbar. Im Wald, Bergen oder Stadt mit schlechterem GPS Empfang können hier deutlichere Abweichungen auftreten. Ausreißer, die in Bewegungsrichtung liegen, können mit dieser topografischen Kontrolle natürlich nicht gefunden werden, obwohl sie auch zu einer Fehleinschätzung der Geschwindigkeit beitragen können.

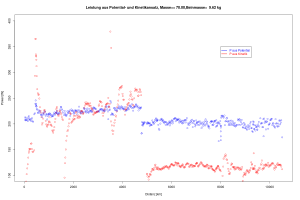
Abbildung 1: Geschwindigkeit und Leistung zu Lauf auf Sportplatz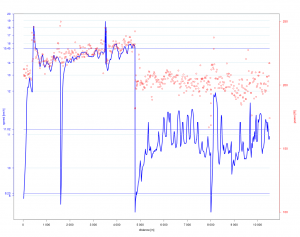

Die Ordinate ist hier nicht äquidistant skaliert, damit das Bild nicht zu sehr von den offensichtlichen Ausreißern am oberen Ende dominiert wird. Für die Luftwiderstandsgleichung ( $v^3$ ) sind diese Werte besonders unangenehm. Deutlich erkennbar sind einige schnellere Runden am Anfang sowie gemütliches Laufen in der zweiten Hälfte. Die dicken blauen Linien sind das 5%, 50%, 95% Quantil der gemessenen Geschwindigkeiten. Mit roten Punkten sind die abgeleiteten Nettoleistungen dargestellt und es lässt sich schon hier ein enger Zusammenhang vermuten.

Exkurs kinetische Energie

Die Arbeit für die Beinbeschleunigung W(Bein) kann nach Rodewald mit

$W_{\mbox{\small Bein}} = \frac{1}{2} m_{\mbox{\small Bein}} v_{\mbox{\small Bein}}^2$

für jeden Schritt geschätzt werden. Das ist die aus der Schulphysik bekannte Gleichung für kinetische Energie, bezogen auf die Beine. Hat der Läufer eine konstante Geschwindigkeit erreicht – „steady state“ d.h. keine weitere Beschleunigung – so ist nach Rodewald

die Beingeschwindigkeit gleich der Laufgeschwindigkeit und
die Energie geht vollständig in den Widerständen (Reibung etc.) auf.

Dies stimmt natürlich nur im Groben. Denn bei jedem Lauf sind abwechselnd die Beine vor und hinter dem Schwerpunkt und müssen deshalb regelmäßig schneller und langsamer sein als der Läufer.

Nach Rodewald kann man die Beinmasse m(B) mit m(B) =1/8 m(Körper) abschätzen. Die Leistung ist dann die Arbeit bezogen auf die Schrittzeit t und damit $P_{\mbox{Bein}} = W_{\mbox{\small Bein}} K$

Rechenbeispiele:
$\begin{tabular}{lrrrr} Masse & 70 & 70 & 70 & 70 \\ Beinmasse & 8,75 & 8,75 & 8,75 & 8,75 \\ \hline Pace [min/km] & 3:20 & 4:10 & 5:00 & 6:00\\ Speed [km/h] & 18 & 14,4 & 12 & 10 \\ v [m/s] & 5,00 & 4 & 3,33 & 2,78\\ \hline WB [J] & 109,38 & 70 & 48,61 & 33,76\\ Kadenz [1/min] & 150 & 150 & 150 & 150\\ Zeit pro Schritt [s] & 0,4 & 0,4 & 0,4 & 0,4\\ \hline P(B) [W] & 273,44 & 175,00 & 121,53 & 84,39 \end{tabular}$

Diese Berechnungen zeigen für hohe Geschwindigkeiten das richtige Niveau. Für niedrige Geschwindigkeiten wie z.B. 6:00 er pace, scheint die Nähe zum Grundumsatz untertrieben.

Abbildung 1a: Gegenüberstellung verschiedener Leistungsberechnungen

Die Gegenüberstellung der zwei Leistungsberechnungsarten zeigt deutliche Unterschiede

in der ersten schnelleren Hälfte stimmen die Leistungswerte zumindest im Mittel noch überein
die langsamere 2 Laufhälfte wird durch das kinetische Modell wahrscheinlich unterschätzt
das kinetische Modell zeigt die größere Streuung.

Berücksichtigt man, dass die Laufgeschwindigkeit mit gps Fehlern behaftet ist, dürften gerade diese durch den Term $v_B^2$ verstärkt werden. Deshalb wird dieser Ansatz zunächst nicht weiter verfolgt.

Beziehung der Leistung zu andere Messwerten der Laufuhr

Die von der Laufuhr aufgezeichneten Felder sind in der folgenden Grafik gegenüber gestellt.

Abbildung 2: Scatterplot zum Lauf auf Sportplatz

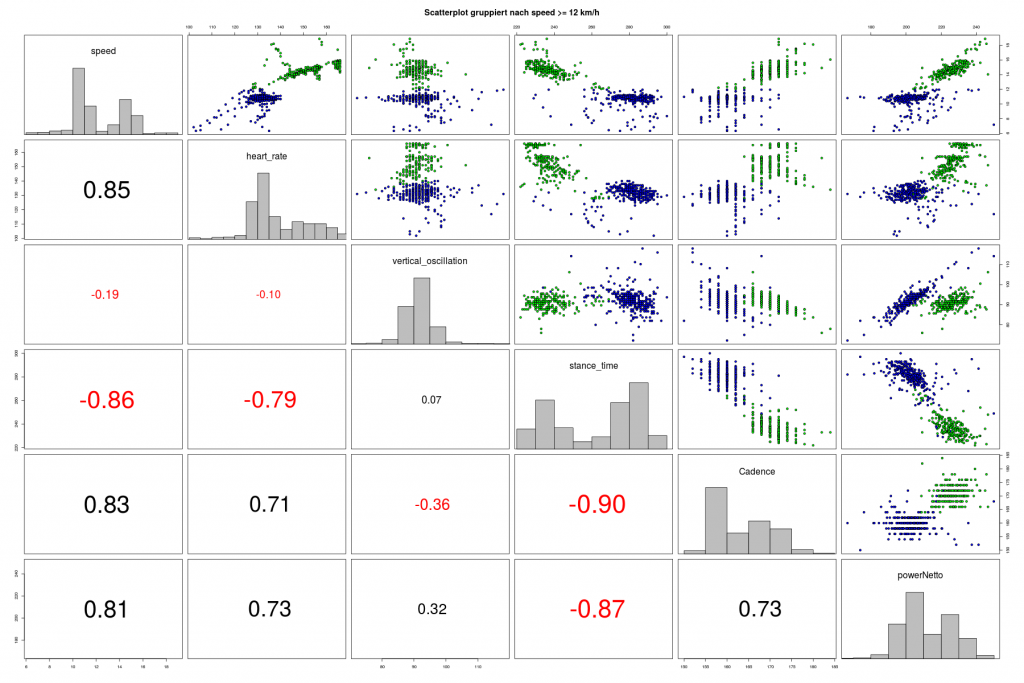
Insgesamt erkennt man auch hier die beiden Laufhälften (kleiner oder größer 12km/h) in allen Beziehungen (oberes Dreieck) gut und es finden sich viele signifikante Korrelationen (unteres Dreieck). Die abgeleitete Leistung ist mit fast allen Größen bis auf den vertikal Hub pro Schritt (vertical oscillation) hoch korreliert. Das war so nicht zu erwarten, da der Löwenanteil der Leistung auf den Aufstieg pro Schritt zurück geht.

Der Scatterplot lässt vermuten, dass man den langsameren und schnelleren Teil des Laufs aufgrund der anderen Variablen gut trennen kann. Dazu wird eine lineares Diskriminanzmodell angesetzt.

Abbildung 2a: Trennung langsamer und schneller Läufe mit lineare Diskriminanzfunktion

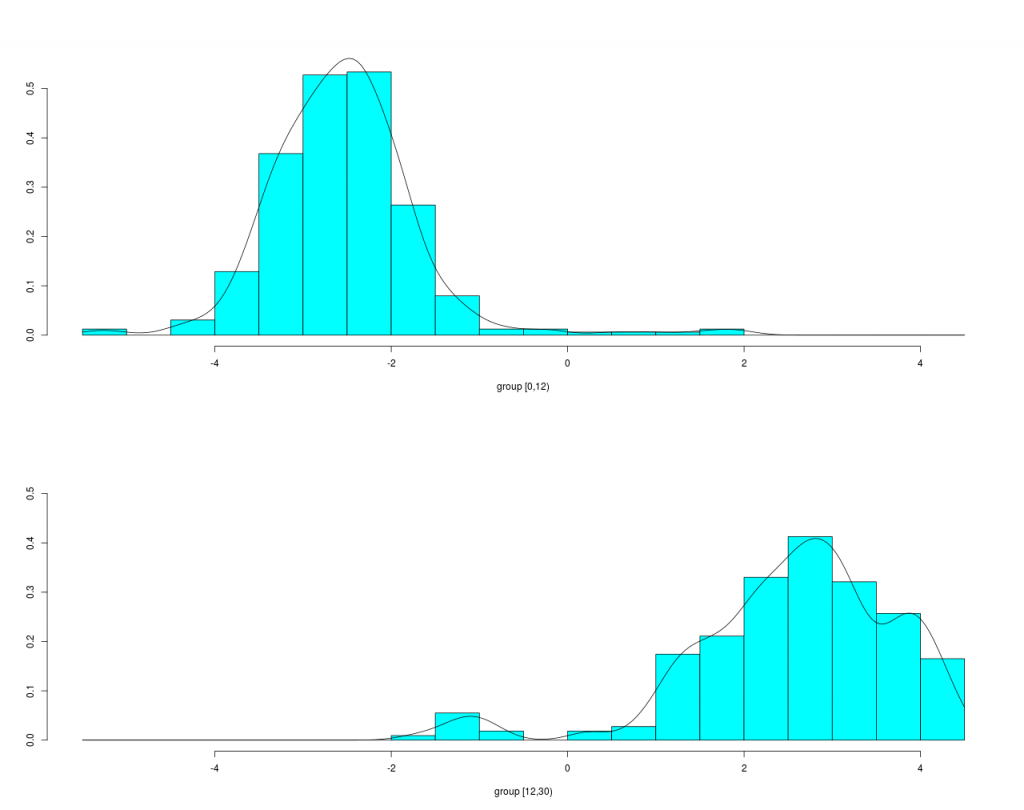
Die Trennebene ist mit dem Vektor

$\begin{tabular}{lr} Variable & LD1 \\ \hline heart\_rate & 0.05344165 \\ Cadence & 0.01522985 \\ stance\_time & -0.08757772 \\ vertical\_oscillation & -0.04386457 \\ \end{tabular}$

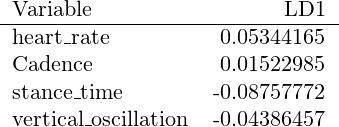
gegeben. Demnach kann man an hoher Herzfrequenz & Kadenz sowie niedriger Bodenkontaktzeit und geringem Vertikalhub langsame von schnellen Läufen relativ gut trennen. Wir haben damit einen empirischen Beleg für weit verbreitete Thesen in der Laufliteratur, die jeder Besitzer einer „neueren“ Laufuhr tagtäglich prüfen kann. Da auch hier die Berechnung für gegebenen LD1 Vektor linear und relativ einfach ist, könnte die Ausgabe auch in Echtzeit erfolgen.

Schätzung der maximalen Leistung

Der Zusammenhang zwischen Leistung und Herzfrequenz soll mit Quantil-Regressionsmodellen weiter untersucht werden. Die Herzfrequenz wird hier als Steuerungsgröße für die Leistung aufgefasst. In der Fachliteratur findet man gelegentlich den Hinweis, dass die Herzfrequenz der Leistung hinterher eilt. Um dies zu prüfen, werden die „gelagten“ Korrelationen power(t), heart_rate(t-L) berechnet.

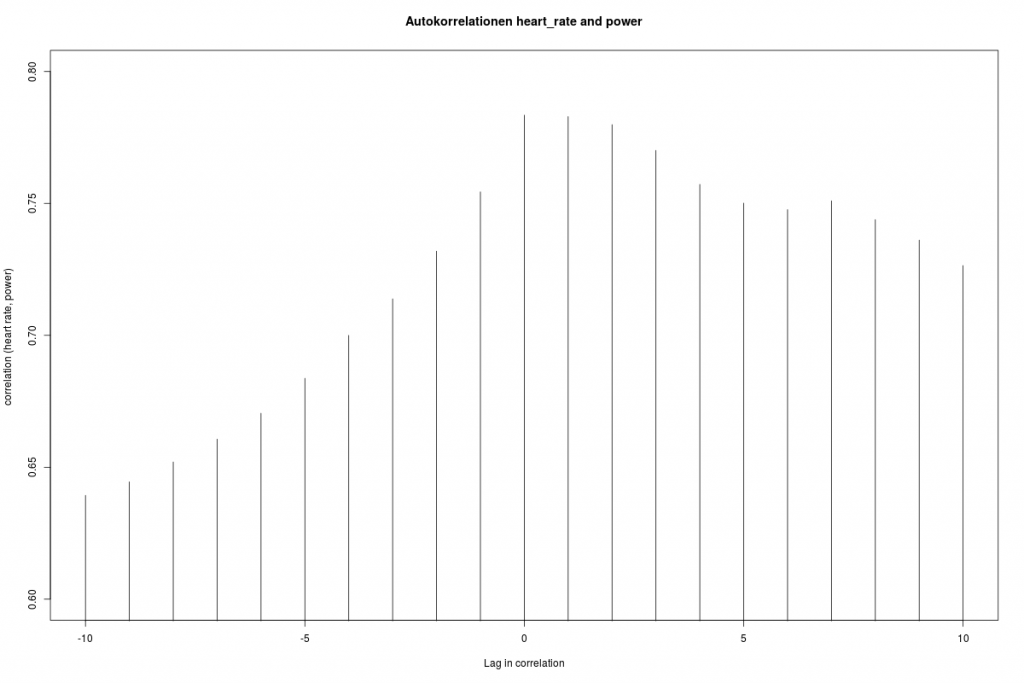
Insgesamt zeigt sich hier schon ein hoher Zusammenhang. Die höchste Korrelation wird beim Lag=0 angenommen: dies spricht für keinen zeitlichen Versatz. Es zeigt sich aber auch, dass ein Lag von 1 kaum zu Einbußen führt. Im Weiteren wird ohne Lag gearbeitet.

Abbildung 3: Leistung und Herzfrequenz

(a) Quantil Regression mit quadratischer Form (b) parametrische Quantil Regression

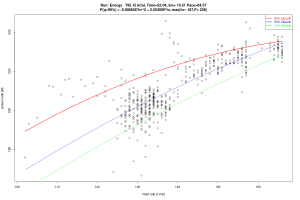
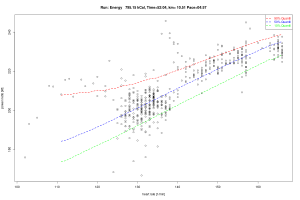
Beide Regressionen zeigen eine mit der Herzfrequenz steigende Leistung.
Bei der quadratischen Form ist diese deutlich degressiv, wobei dies sicherlich auch an der vorgegebenen Funktionsform liegt. Ferner lässt sich ein Leistungsmaximum bei ca. 230 Watt erahnen. Das stimmt auch relativ gut mit der oberen Leistungsgrenze für 1 Std Radfahrt beim Autor überein.
Bei der parametrischen Regression kann man zwar auch eine Leistungsdegression erahnen, das Maximum dürfte demnach aber Höher liegen. Das wiederum deckt sich ganz gut mit der Pace im 10km Wettkampf des Autors, die höher liegt und in dieser Runde nicht erreicht wurde.

Zerlegung der Geschwindigkeit in Einflussgrößen

Abschließend soll der Einfluss dieser Variablen auf das Tempo identifiziert werden. Dazu wird ein IRLS Ansatz für ein Regressionsmodell gemacht.

Abbildung 4: Regressionsmodell zur Identifizierung der geschwindigkeitsbestimmenden Variablen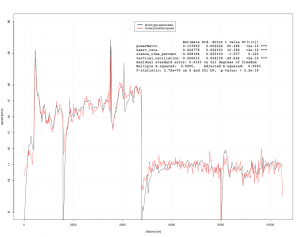

Sämtliche Koeffizienten haben das fachlich erwartete Vorzeichen, auch wenn „stance_time_percent“ nicht signifikant ist. Dies wird auch an der im Scatterplot deutlich erkennbaren negativen Korrelation liegen. Der größte Einfluss geht von der Leistung aus, gefolgt von der Herzfrequenz. „vertical_oscillation“ also der Vertikalhub pro Schritt hat ein negatives Vorzeichen, was auch den Theorien entspricht. Die Kadenz konnte nicht mit einbezogen werden, da sie hoch mit power korreliert ist (vgl. power Ableitung) und damit nicht sicher zwischen beiden Einflüssen unterschieden werden kann.

Ausblick

Das vorgestellte Leistungsmodell basiert im wesentlich auf Vertikalhub, Kadenz und Geschwindigkeit des Läufers, die in Echtzeit messbar sind. Für einen weiteren Ausbau des Modells

sollten die anderen physikalischen Modelle zum Gehen und Laufen wie. z.B. kinetischer Ansatz, umgekehrtes Pendel, Feder-Masse-Modell geprüft werden
sollte man insbesondere stärker physiologisch orientierte Modelle untersuchen, denn dieser Aspekt ist hier mit dem Wirkungsgrad η und Herzfrequenz nur sehr rudimentär abgebildet.
sollte der Absprungwinkel ϕ weiter betrachtet werden, zumal er sich ebenfalls aus den Daten der Laufuhr abschätzen lässt
sollten Auf- und Abstiege einbezogen werden
das Modell an einer breiteren Datenbasis kalibrieren. Dazu könnte man im Lauftreff Messungen bei den Mitgliedern durchführen und im Rahmen einer Querschnittanalyse das Modell anpassen und ergänzen.

Literatur

Müller, R. (2006) Die Physik des Gehens als Unterrichtsfach, TU Braunschweig
https://www.tu-braunschweig.de/Medien-DB/ifdn-physik/gehen-und-laufen.pdf

Rodewald, B. u. H.J. Schlichting (1988) Springen, Gehen, Laufen, Praxis der Naturwissenschaften-Physik 37/5 (1988) S. 12-14
https://www.uni-muenster.de/imperia/md/content/fachbereich_physik/didaktik_physik/publikationen/springen_gehen_laufen.pdf

Rottler, A. (2014) Dr. Lälles erklärt’s
http://www.laufen-in-siegen.de/index.php/dr-laelles-erklaert-s/laelles-uebersicht

Waller, D. (2008) Physics meets Sports: Biomechanische Modelle Gehen und Laufen
http://tennisfragen.de/wordpress/wp-content/uploads/2011/11/Gehen-und-Laufen-Waller-UNI-Regensburg.pdf

Weidt, M. und T. Wilhelm (2015) Gehen und Laufen im Physikunterricht
http://www.thomas-wilhelm.net/veroeffentlichung/Gehen.pdf

Tag Archives

Laufleistung in Watt