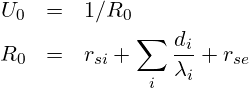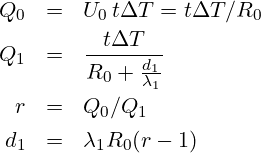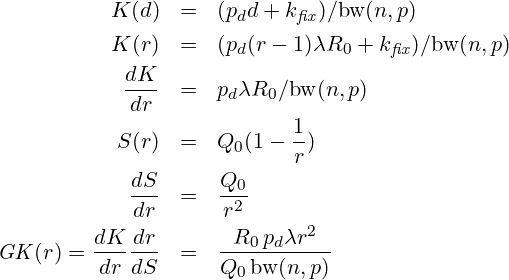Klimatische Einordnung Langenfeld in den EU-Kontext
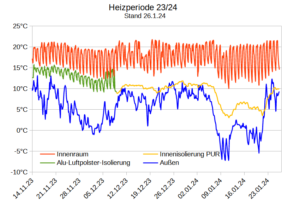
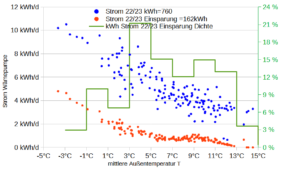
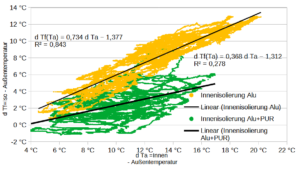
In der politischen Diskussion um das GEG werden energetische Sanierung und Wärmepumpen als Maßnahmen zur C02 Reduktion im Haushalt von der derzeitigen Ampel-Regierung favorisiert. Beides hängt mit dem Heizbedarf im Haus zusammen. Zu Kennzeichnung des Wärmebedarfs gibt es auf EU-Ebene 3 Regionen „colder-“, „average-“ und „warmer region“ für die normierte Heizstundenverteilungen (Heizstunden bei T °C) vorliegen. Diese werden benutzt um aus den verschiedenen COP-Werten einer Klimaanlage den SCOP herzuleiten. Aus dem Winter 2022/2023 habe ich Temperaturmessungen vor Ort während der Heizzeit gesammelt und den Temperaturverteilungen „average“ und „warmer region“ gegenübergestellt, vgl. Grafik.
Die Grafik oben zeigt, dass meine Messungen zu Langenfeld (grüne Linie) zwischen „average“ und „warmer“ liegt. Meine Messungen beziehen sich nur auf die Heizzeit, wenn das Gerät angeschaltet war. Nachts hatte ich es so gut wie nie eingeschaltet. Nur 2,3% der Heizstunden lagen 2022/23 im Frostbereich. Das sind dann die Tage, an denen die Wärmepumpe eine hohe Energieaufnahme hat.
Wie im vorherigen Beitrag schon vermutet, geht der dort berechnete sehr gute SCOP>5 auch auf diese für Wärmepumpen günstige Temperaturverteilung zurück. Die globale Erwärmung dürfte auch in Langenfeld für eine weitere Rechtsverschiebung der Verteilung sorgen. Die Häufigkeit der Frosttage dürfte weiter abnehmen, was ja auch dem langfristigen Trend entspricht, der sich nicht zuletzt auch in der Biosphäre (Vogelzug) als auch in der Landwirtschaft (Blühbeginn, Schädlinge) bemerkbar macht. Für das Jahr 2023 meldet der DWD eine Durchschnittstemperatur für Deutschland von 10,6°C, der höchste Wert seit Aufzeichnung 1881.
Vor dieser Perspektive muss man auch die Wärmedämmung beurteilen. Die Vermutung, dass diese Temperaturentwicklung die Rentabilität der Dämmung drückt, liegt auf der Hand. Gleichzeitig fördert dies die Effizienz (SCOP) der Wärmepumpe. Die Relationen verschieben sich. Offen ist hingegen die Frage, wie lange der Gesetzgeber braucht, um dies zu antizipieren. „Die Planwirtschaft in ihrem Lauf, hält weder Ochs noch Esel auf„…
Zentrales Maß der Dämmung: der U-Wert
Das zentrale Maß für die Dämmung ist der U-Wert der Außenhülle eines Gebäudes. Kennt man den Wandaufbau, kann man unter Ubakus.de den U-Wert [W/qm/K] berechnen.
Ich habe das für meine Außenwand mit Ubakus.de und Excel gemacht und komme für eine 48cm zweischalige Vollziegelwand auf eine Wert von 1,08 W/qm/K.
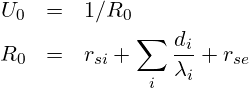
An der U-Wert Gleichung erkennt man, dass der Wärmeverlust unabhängig von der Schichtanordnung i ist. Innen-, Einblas- oder Außendämmung unterscheiden sich nicht im Wärmeverlust wenn Material und Schichtdicke identisch sind.
Diese kann man nun beispielsweise mit XPS (Styropor) dämmen, das eine λ =0,035 W/m/K hat.
![\[ U_1 = 1/(R_0 + \frac{d}{\lambda} ) = \frac{\lambda }{\lambda R_0 +d}\]](https://lt-pappelallee.de/wp-content/ql-cache/quicklatex.com-8d164164c720379aa8603e9d6ef3eec0_l3.png "Rendered by QuickLaTeX.com")
Die verlorene Wärme Q_0 ist dann Q_0 = U_0*t*ΔT wobei t die verstrichene Zeit und ΔT die Temperaturdifferenz ist.
Möchte man nun die Wärmeabgabe Q0 um den Faktor r reduzieren so ergibt sich:
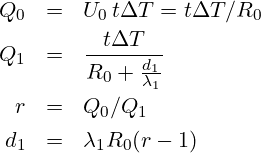
Diese Gleichung für die Dämmstärke ist unabhängig von der verstrichenen Zeit t und der Temperaturdifferenz ΔT was für Alltagsrechnungen nützlich ist. Ist z.B. R_0=1 und möchte man den Heizbedarf mit Styropor ( λ =0,035 ) halbieren (r=2) so brauche ich dafür 0,035m = 3,5cm.
Möchte man zusätzlich die Energieeinsparung S(d) der Dämmung d berechnen, braucht man noch den historischen Heizbedarf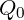 
für die Wand:
![\[ S(r(d)) = Q_0-Q_1 = Q_0 \frac{r-1}{r}\]](https://lt-pappelallee.de/wp-content/ql-cache/quicklatex.com-78692b0daab9e744c8cda48089eace21_l3.png "Rendered by QuickLaTeX.com")
In ist dann das historische Heizverhalten und ΔT abgebildet.
Dämmungsvarianten mit Wärmepumpe
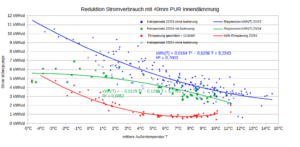
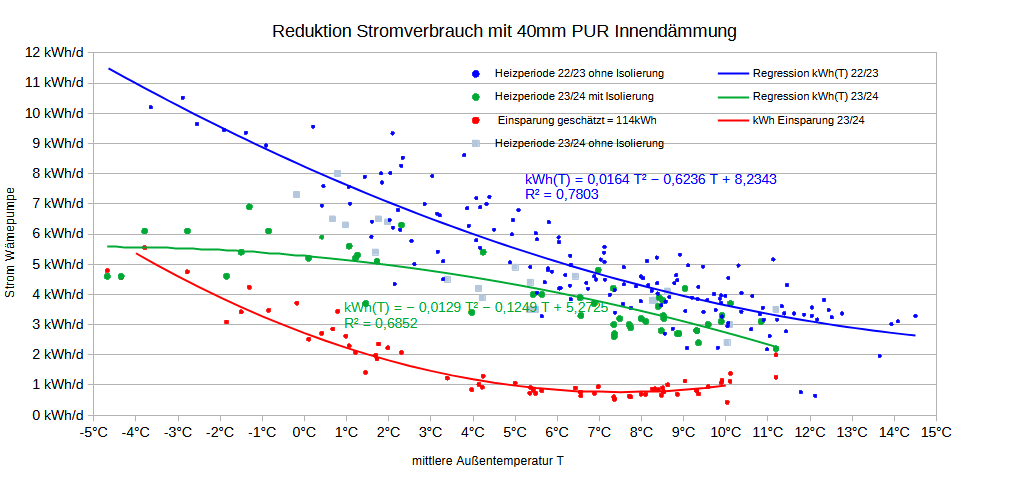
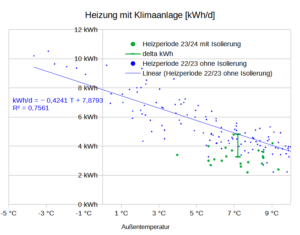
Wenn ich nun meine Heizstunden aus 2022/23 sowie eine mittlere Temperaturdifferenz zwischen Innen- und Außen Temperatur von 15 °C unterstelle – was mehr ist als 2022/23 gemessen – kann man den Wärmeverlust je qm in Abhängigkeit der Dämmstärke berechnen. Diesen Wärmeverlust muss man mit der Heizung entgegen treten, wenn man die Raumtemperatur bei angenehmen 19°C halten will. Ich habe das letztes und dieses Jahr mit einer Klimaanlage gemacht und gehe hier von einem SCOP=4 aus (der im vorherigen Beitrag geschätzte Wert war höher).
Man sieht am U-Wert in Abhängigkeit der Dämmstärke den charakteristisch degressiv fallenden Verlauf, da die Dämmstärke im Nenner des U-Werts steht. Die eingesparten kWh -Strom zeigen spiegelbildlich einen degressiv steigenden Verlauf in Abhängigkeit der Dämmstärke. Ökonomisch spricht man von abnehmenden Grenzerträgen.
Eine Dämmung von 200mm XPS reduziert hier den Stromverbrauch um ca. 10 kWh/qm/a. Nun fallen die Stromeinsparungen jährlich an, die Investition in die Dämmung ist aber – hoffentlich – einmalig. Um beides miteinander vergleichen zu können, brauche ich den Barwert (NPV) der Einsparungen.
Überschlagsrechnung: Gehe ich von 5% Zinsen aus, unterstelle einen Strompreis von 40ct/kWh und eine unendliche Haltbarkeit der 200mm Dämmung so ist NPV= 0,4 * 10/ 0,05 = 80 €/qm. Schaut man auf den Markt (myhammer) oder in aktuelle Literatur (Verbraucherzentrale) ist klar, dass man für diesen Betrag keine Außendämmung montiert bekommt. Wenn man es dennoch macht und von realistischen 160 €/qm ausgeht, läuft man ins Defizit (wie die Politik, vgl. aktuelle Haushaltsdiskussion in Deutschland).
Wenn wir nun abweichend von einer Haltbarkeit von 40 Jahren ausgehen, Kosten von 160 €/qm unterstellen und mit einem Zins von 5% rechnen ergibt sich:
AFA = 160/40 € /Jahr = 4 €/Jahr/qm
Zinsanspruch = 160*5% = 3,2 €/ Jahr/qm
Summe der Kosten = 7,2 € / Jahr/qm
Die Einsparungen betragen aber nur 4 € / Jahr/qm, also nicht rentabel, und decken gerade die AFA.
Grenz- und Durchschnittskosten der Dämmung
Im folgenden wird diese Abschätzung quantitativ abgeleitet. Für die ökonomische Analyse brauchen wir die Kosten K, die Grenzkosten GK der Wärmeeinsparung/produktion S durch Dämmung d, also d K/ d S.
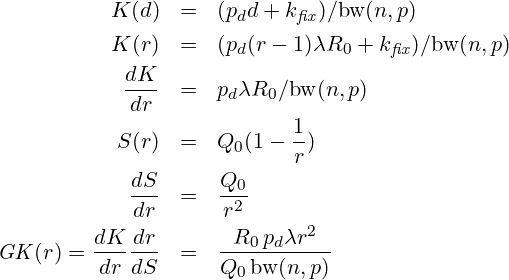
mit: d=Dämmstärke in m, pd=Preis der Dämmung 260€/cbm, kfix=Montagekosten/qm, bw(n,p)= Barwert bei n=40 Jahren zu p=5% Zinsen, λ=Wärmeleitfähigkeit Dämmung, Q0 = Wärmeverlust ungedämmt, R0 Wärmewiderstand ungedämmt, r Reduktion des Wärmeverlust
Diese Zusammenhänge sind im Folgenden grafisch dargestellt.
Für den Graph „Eigenleistung“ habe ich einen Lohnansatz von 12 €/qm angesetzt. Bei einer Dämmstärke von 40 mm XPS zu 260 €/cbm komme ich auf Materialkosten von 0,04*260= 10,40€/qm in Summe also 10,40+12,00 = 22,40€/qm. Bei einer Nutzungsdauer von 40 Jahren und einem Kalkulationszinssatz von 5% ist der Barwertfaktor=17,16. Damit entspricht diese einmalige Investition einer jährlichen Zahlung von 1,31€/a/qm.
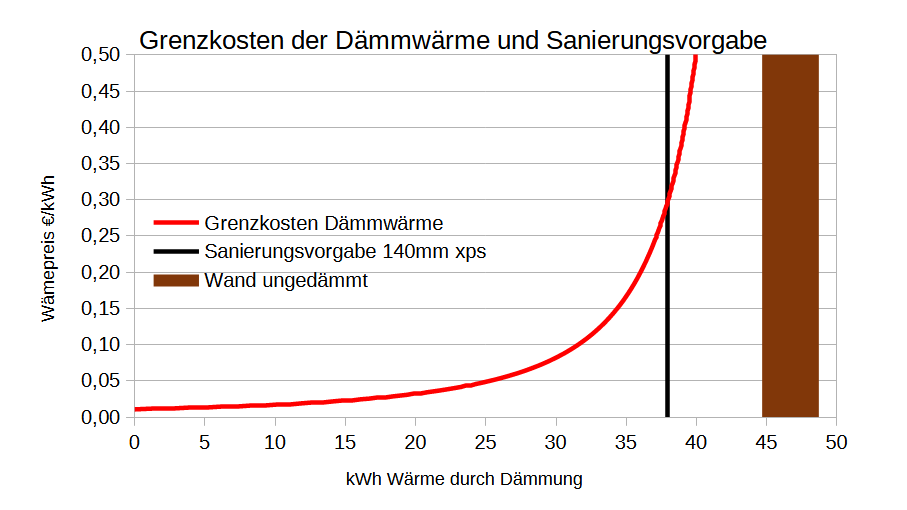
Bei einem Ausgangs U-Wert von 1,08 und einem Gesamtwärmewiderstand R0=0,9245 und 2880 Heizstunden bei durchschnittlich 15°C Temperaturunterschied beträgt die Ausgangwärme Q0=46,73 kWh/a. Der Reduktionsfaktor r beträgt bei dieser Dämmung nach obiger Formel 2,36 so dass man damit 46,73*(r-1)/r = 25,83 kWh/a/qm spart. Bezogen auf die jährlichen Kosten von 1,31€/a/qm hat man also Wärmekosten von 0,051 € /kWh. Da die Durchschnittskostenkurve stets im Minimum von den Grenzkosten geschnitten wird sind dies auch die Grenzkosten. Bei einem SCOP von 4 und 40ct/kWh Strom= 0,10€/kWh Wärme könnte ich also noch gewinnbringend weiter dämmen bis ca. 70mm xps.
Ganz anders sehen die Wärmekosten bei Vergabe des Isolierauftrags zu 120€/qm Montagekosten aus, vgl. blaue Linie. Hier kommt es mindestens zu 0,24 € /kWh also knapp das 5-fache an Kosten. Jede Klimaanlage kann das günstiger. Weiterhin ist dies das doppelte des derzeitigen Gaspreis’. Da man dann dauerhaft auf hohen Wärmegestehungskosten sitzt, hat dies zur griffigen Formulierung „verdämmt in alle Ewigkeit“ geführt.
Die Dämmung wird politisch mit der sich abzeichnenden Erderwärmung begründet. In der Grafik oben stellen die gepunkteten Linien die Kostenfunktionen für eine Abnahme der Temperaturdifferenz um 1,5°C (=-10% Ausgangslage) da. Mathematisch schlägt sich dies in der Gesamtenergie Q0 nieder. Einen zur Erderwärmung gleichen Effekt würde man mit einer Verkürzung der Heizzeit um 10% erzielen. Empirischer Beleg dafür ist die Verschiebung des Blühbeginns in der Vegetation. Als Resultat wird die Grenzkostenkurve noch ungünstiger und die Durchschnittskosten steigen. Auch hier erweist sich die Eigenleistung als stabiler gegenüber der Auftragsvergabe. Nicht nur der Erwartungswert sondern auch die Streuung der Wärmekosten ist geringer, so dass man hier von stochastischer Dominanz ausgehen kann.
Umgekehrt kann man eine starke Dämmung auch als Wette auf kalte und lange Winter interpretieren (die Grenzkostenkurve verschiebt sich nach rechts), da in dieser Konstellation die Rentabilität steigt. Empirisch gibt es dafür aber derzeit keinen Anhaltspunkt. Weitere Dämmung ist vor dem Hintergrund Erderwärmung ökonomisch irrational.
Eine weitere wesentliche Unsicherheit geht von der Haltbarkeit der Dämmung aus. Die hier unterstellten 40 Jahre ohne weiteren Aufwand sind schon recht optimistisch. Ich bin deshalb mal abweichend davon von nur 20 Jahren ausgegangen, vgl. Grafik.
Auch in diesem Fall ist die Eigenleistungslösung dominant überlegen und auch noch rentabel. Für die Auftragslösung ist das Urteil: 20 Jahre überhöhte Wärmekosten. Wenn man dann noch in Betracht zieht, die marode Dämmung zu entsorgen und durch eine neue – für die dann geltenden Montagekosten – zu ersetzen gilt: Verdämmt in alle Ewigkeit.
Mikroökonomische Interpretation
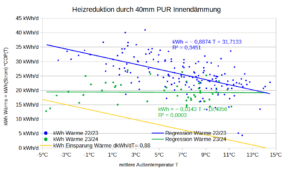
Für die Dämmung gilt das Gesetz vom abnehmenden Ertragszuwachs. Die letzten mm führen kaum noch zu Energieeinsparungen,vg. Grafik Dämmungsvarianten.
Die ungedämmte Wand kann man als endliche Energie-Ressource begreifen, deren Energie man bei kalten Tagen mit Dämmung fördert. Sie ist bei einer Temperaturdifferenz ΔT = 0,0 erschöpft. Es lohnt sich nicht, die letzten Energieeinheiten zu fördern, weil die Grenzkosten dafür enorm ansteigen, vgl. Titelbild. Das sogenannte „Energieeffizienzhaus“ wird diese Abbauwürdigkeit vermutlich weit überschreiten.
Ein andere Parallele kommt aus dem PV-Bereich und der Frage, wieviel kWh Akku sinnvoll sind. Wenn man den Akku durch seinen Verbrauch nicht genügend & regelmäßig auslastet, sinkt bekanntlich die Rentabilität des Stromspeicher. Für saisonalen Ausgleich z.B. über 6 Monate ist der Akku nicht rentabel und man braucht andere Speichertechniken (z.B. H2).
Die Parallele zur Dämmung ergibt sich aus der Temperaturdifferenz ΔT. Tritt ΔT nicht häufig oder großgenug im Kalkulationszeitraum auf, sinkt die Rentabilität wie das Szenario „+1,5°C“ gezeigt hat. Die Temperaturbeobachtungen der letzten Jahre sowie die Einordnung des Standort Langenfelds in den EU-Kontext (vgl. oben), dürfte die Rentabilität starker Dämmungen eher senken.
Volkswirtschaftliche Aspekte der Dämmung
Diese hohen Wärmegestehungskosten der Dämmung wird im Mietverhältnis der Vermieter auf den Mietpreis aufschlagen wollen. In der politischen Debatte wird dies derzeit vornehmlich vor dem Hintergrund „sozial“ bzw. den Verteilungseffekten diskutiert. Faktisch geht es damit fast nur noch um die Frage, wer auf den Kosten der übermäßigen Dämmvorgaben sitzen bleibt. Es drängt sich die Vermutung auf, dass dies der Grün-Rote Kompromiss der Ampel-Regierung ist, in dem „soziale Flankierung“ eine Umschreibung für „der Eigentümer soll auf den Dämmkosten sitzen bleiben“ ist.
Unabhängig von der Verteilungsfrage scheint der Grad der optimalen Dämmung kaum zu interessieren. Wird unsere ganze Volkswirtschaft durch Gesetzte / Verordnungen in diese übertriebene Dämmung der Bestandsimmobilien (der Wert dürfte im Billionenbereich liegen) gedrängt, ergeben sich enorme Wohlstandsverluste. Diese entstehen auch daraus, dass das Kapital anderen produktiveren Bereichen (z.B. Wohnungsbau) entzogen wird und in unrentable Dämmung investiert wird. Mit einer Verzögerung wird sich dieser Effekt auch beim Fiskus bemerkbar machen. Einerseits schrumpfen die Einnahmen aus Energiesteuern, andererseits gehen Steuern auf Erträge der alternativen Kapitalverwendung zurück.
Für den Einzelnen mag sich dank Subvention (GEG) eine solche Dämmung dann noch gerade rechnen, volkswirtschaftlich bleibt es aber ein Mrd. € Grab. Der Gesetzgeber vernichtet damit Wohlstand.
Die Politik wäre gut beraten, wenn sie diese quantitative Allokationsfrage – Abwägung zwischen Dämmung und Energieerzeugung – den Haushalten und Unternehmen überlassen würde. Ein Energiepreis, der auch externe Umwelteffekte reflektiert, wird zu einer besseren Allokation führen als die derzeit starren technischen Dämm- oder SCOP-Vorgaben. Er spart zudem auch an Verwaltungsaufwand.
Eigene Dämm-Abwägungen
Diese geschätzte geringe bis negative Rentabilität der Dämmung kann man nun verbessern:
- man reduziert die Dämmstärke um in einen steileren Bereich der U-Kurve zu kommen.
- man reduziert die Einbaukosten in dem man viel Eigenleistung einbringt (vgl. oben).
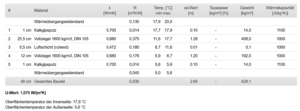
Für meine Außenwand U=1,08 W/qm/K, einer XPS-Dämmung zu 260 €/cbm mit λ=0,035, einem Zins von p=5%, Stromkosten von 40 ct/kWh und SCOP=4, und einem Eigenlohnansatz von 12 €/qm habe ich das in der folgenden Tabelle dargestellt:
|
Dicke [mm]
|
Eingesparte kWh/Jahr/qm
|
Dämmstoffkosten
|
Kosten Total
|
Kosten Total/Einsparung
|
Amortisationszeit
|
|
0
|
0,00
|
|
|
|
|
|
5
|
6,25
|
1,30
|
13,30
|
2,127
|
1.000,00
|
|
10
|
11,03
|
2,60
|
14,60
|
1,324
|
22,00
|
|
15
|
14,80
|
3,90
|
15,90
|
1,074
|
15,50
|
|
20
|
17,85
|
5,20
|
17,20
|
0,964
|
13,00
|
|
25
|
20,37
|
6,50
|
18,50
|
0,908
|
12,00
|
|
30
|
22,48
|
7,80
|
19,80
|
0,881
|
11,50
|
|
35
|
24,28
|
9,10
|
21,10
|
0,869
|
11,50
|
|
40
|
25,83
|
10,40
|
22,40
|
0,867
|
11,50
|
|
45
|
27,18
|
11,70
|
23,70
|
0,872
|
11,50
|
|
50
|
28,37
|
13,00
|
25,00
|
0,881
|
11,50
|
|
55
|
29,42
|
14,30
|
26,30
|
0,894
|
12,00
|
|
60
|
30,35
|
15,60
|
27,60
|
0,909
|
12,00
|
Die Dämmung mit den geringsten Durchschnittskosten und damit mit der kürzesten Amortisationszeit liegt bei ca. 40mm.
Das ist für eine Innendämmung noch ein erträgliches Maß. Wenn ich das in die oben abgeleitete Gleichung d=λ R(r-1) einsetze und nach r auflöse komme ich auf eine Reduzierung der Heizkosten für diese Außenwand um den Faktor 2,36 also mehr als halbiert.
Welchen Einfluss hat der Energiepreis p auf die Dämmung d bei dem Kriterium Amortisationszeit?
Jede Dämmstärke d_i führt unabhängig vom Energiepreis zu einer Einsparung von kWh_i. Der Quotient aus eingesparten Kosten kWh_i * p und investiertem Kapital ist linear homogen im Energiepreis d.h. der Energiepreis hat keinen Einfluss auf die Wahl der Dämmstärke. Günstiger, selbstproduzierter PV-Strom beeinflusst also in diesem Modell nicht die Wahl der Dämmstärke. Ebenso verhält es sich mit der CO2 Abgabe auf Erdgas.
Bei den Dämmstoffkosten (hier 260 €/cbm) sieht es jedoch anders aus: je billiger desto mehr Dämmung. Auf der anderen Seite gilt: je „ökologischer“ und teurer, desto weniger Dämmung.
Analog zur mehrwertsteuerbefreiten PV, könnte die Politik auch hier unbürokratisch den Preis senken um die Dämmung zu fördern.
Welchen Einfluss hat der Energiepreis p auf die Dämmung d bei dem Kriterium Grenzkosten?
Wähle ich das Kriterium Grenzkosten zur Bestimmung der optimalen Dämmung hat der Energiepreis natürlich einen Einfluss auf die Dämmstärke und es gilt Grenzkosten der Dämmung= Grenzkosten der Wärmeproduktion. Genaugenommen braucht man dann aber eine Erwartungshaltung zu den zukünftigen Energiepreisen, was erheblich Varianz in die Betrachtung einbringt. Man hat den Eindruck, dass in der politischen Diskussion diese Unwägbarkeit für die Verschleierung der geringen Rentabilität der Dämmung genutzt wird: Nur die dümmsten Schafe wählen ihren Metzger selber.
Wie steht die Dämmung zur Wärmepumpe und PV?
Im Winter 2022/23 habe ich ca. 30% des Stroms mit der eigenen PV produziert. Meinen internen Strompreis habe ich wie folgt angesetzt ps=30%*0,10 + 70%*0,40= 0,31 €/kWh.
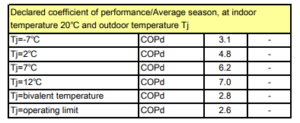
Für die Klimaanlage unterstelle ich einen SCOP=4, Kosten von 1200€ und eine Haltbarkeit von 40000 kWh Wärme. Die Grenzkosten der Wärmeproduktion sind dann (0,31+1200/40000)/SCOP=0,11 €/kWh Wärme. Zu diesem Wärmepreis kann man nicht viel dämmen, vgl. Grenzkosten. Es sind dann ca. 70mm XPS Dämmung optimal, vgl. Grafik. Bei der Eigenleistungslösung bin ich dann im Plus, bei der Vergabelösung tief im Minus. An dieser Rechnung erkennt man weiterhin, dass PV, Klimaanlage und Dämmung Substitute sind:
- je mehr PV und/oder desto günstiger der Strom,
- je effizienter die Klimaanlage d.h. desto günstiger die Wärme
- desto weniger Dämmung.
Wie sieht die Ökobilanz der Dämmung aus?
Eine 40mm starke Dämmung /qm entspricht 0,04* 1 = 0,04 cbm. Unterstellt man 500 kWh/cbm in der Herstellung der Dämmung, führt dies einmalig zu 20kWh Energieaufwand. Da ich derzeit einen Ökostromtarif habe (100% erneuerbare Energie, so das Werbeversprechen) verschlechtert das meine CO2 – Bilanz rein rechnerisch. Das ist auch bei einem Haushalt mit Wärmepumpe und Ökostrom nicht anders zu erwarten, und ich frage mich, ob das dem Gesetzgeber klar ist. Das soll jetzt die Politik nicht zu weiteren Markteingriffen – Verbot von XPS, PUR, PIR, Glas- und Steinwolle – animieren.
Substitution Dämmung versus Wärmepumpen
Mit der Dämmung kann ich Energie sparen, das gleiche gilt für den SCOP des Heizgeräts. Damit liegt eine substitutive Beziehung zwischen diesen beiden Investitionen vor, im Gegensatz zu der vielfach in Medien formulierte komplementären Beziehung, dass nur beides zusammen Nutzen stiftet.
Der Energieaufwand E(Dämmung,SCOP) = Q(Dämmung)/SCOP=U(Dämmung)*t*Δ T/SCOP.
In der folgenden Tabelle ist der Energieverbrauch kWh/a/qm für Polyurethan (PUR) Dämmung für meine Außenwand U=1,08 dargestellt.
|
Dämmstärke d in mm λ=0,023
|
|
SCOP
|
0,00
|
21,26
|
42,53
|
63,79
|
85,06
|
148,85
|
|
1
|
46,73
|
23,36
|
15,58
|
11,68
|
9,35
|
5,84
|
|
2
|
23,36
|
11,68
|
7,79
|
5,84
|
4,67
|
2,92
|
|
3
|
15,58
|
7,79
|
5,19
|
3,89
|
3,12
|
1,95
|
|
4
|
11,68
|
5,84
|
3,89
|
2,92
|
2,34
|
1,46
|
Demnach führt ein SCOP von 4 im ungedämmten Zustand führt auf den gleichen Energieverbrauch wie eine Dämmung mit d= 63,79mm PUR bei SCOP=1. Die Paare (SCOP=4 ; 21,26mm) und (SCOP=1 ; 148,85mm) sind ebenfalls energetisch gleichwertig. Sind sie es auch ökonomisch gemessen in EURO? Die erste Variante bekomme ich mit Klimaanlage und 2cm Innendämmung (Eigenleistung), die zweite Variante mit massiver Außendämmung, Gerüstbau und Handwerkerkosten. Aus den Grenzkostenbetrachtungen der Wärmeproduktion im vorherigen Abschnitt wissen wir, dass die Wärmepumpe um ein vielfaches günstiger die Wärme produziert als massive Dämmung sie einspart.
In der Grafik oben, ist die Substitutionsbeziehung zwischen SCOP und d dargestellt. Die gebogenen Höhenlinien und Farben geben den Energieverbrauch für meine Außenwand an. Als Ökonom drängt sich hier die Frage der optimalen Intensität (Faktor/Faktor-Verhältnis) auf, hier Wärmepumpe und Dämmung. Aus dem 1. Semester wissen wir, dass im Optimum die Tangenten an die Höhenlinien dem reziproken Preisverhältnis entsprechen. Oder: Bei vorgegebenem Budget steht der Gradient der Kostenfunktion senkrecht auf der Budgetrestriktion (Kuhn Tucker Bedingung).
Wenn man das nach obiger Gleichung auswertet, kommt man auf einen linearen Expansionspfad. Dieser ist unabhängig von der Konstanten c die hier für t * ΔT steht d.h. für die optimale Intensität spielt Heizperiode t und Temperaturhub ΔT keine Rolle.
Ein Pfad davon – Parameter K – ist in der Grafik als Gerade eingezeichnet. Damit kann man zunächst qualitativ eine optimale Richtung abschätzen.
Beispiele
- Du hast 2 „linke Hände“ oder kannst/willst keine Eigenleistung einbringen. Die Dämmung ist dann relativ teuer gegenüber der Klimaanlage. Dann wählt man im Optimum wenig Dämmung und viel Klimaanlage. Meine Diskussionen mit Bekannten zum Energiesparen lassen aber eher die andere Richtung erkennen. Diese sind mehrheitlich eher der Dämmung zugeneigt als der Wärmepumpe und bestellen sich lieber noch schnell einen Gasbrennwertkessel, bevor das GEG hier einen Strich durch macht. Ist das die Furcht vor einem übergriffigen Staat? Der Gasbrennwertkessel hat aber eine Gesamtenergieeffizienz von unter 1. Fasst man den Energiebilanzraum sehr weit d.h. misst Gesamtenergie (primär Energie + Heizungspumpe, Warmwasser etc.) und bezieht das auf die nutzbare Wärme Q, so dürfte sich derzeit eher eine Effizienz von 0,80 – 0,85 beim Gasbrennwertkessel einstellen. Des weiteren ist nach „Merkel“-Fahrplan mit einer Erhöhung der CO2-Abgaben zu rechnen.
- Du hast schon viel gedämmt, weil Dich das Gesetz / Verordnung im Neubau dazu gezwungen hat. Die entscheidungsabhängigen Kosten der Dämmung sind also 0,0 €/qm und du sitzt auf „versunkenen Kosten“. Dann wird man nicht mehr viel in den SCOP investieren wollen. Das billigste ist dann derzeit eine Infrarotheizung bei der man keinen Installateur braucht und diese einfach in die Steckdose steckt. Schornsteinfeger, Heizungswartung, hydraulischer Abgleich, Grundgebühr Gasanschlusse etc. spart man dann auch. Weiterhin liefert die Infrarotheizung angenehm empfundene Strahlungswärme.
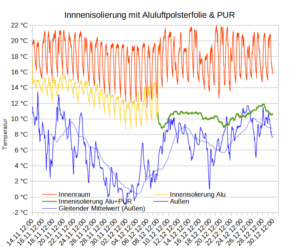
Ich habe mich für eine gemischte Strategie entschieden: SCOP=4 und d=40mm PUR (λ=0,023) + 3mm Aluluftpolsterfolie. Diese gemischte Dämmung hat den gleichen Wärmewiderstand wie ein 7cm xps Dämmung. Ich brauche dann ca. 8 kWh Strom/qm/a Davon kann ich ca. 30% in der Heizperiode mit PV bereitstellen.
