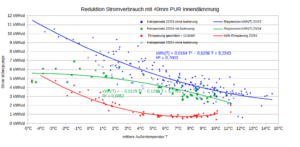
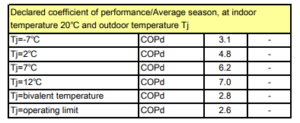
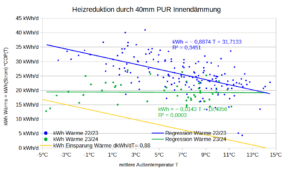
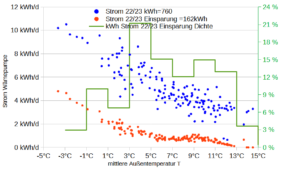
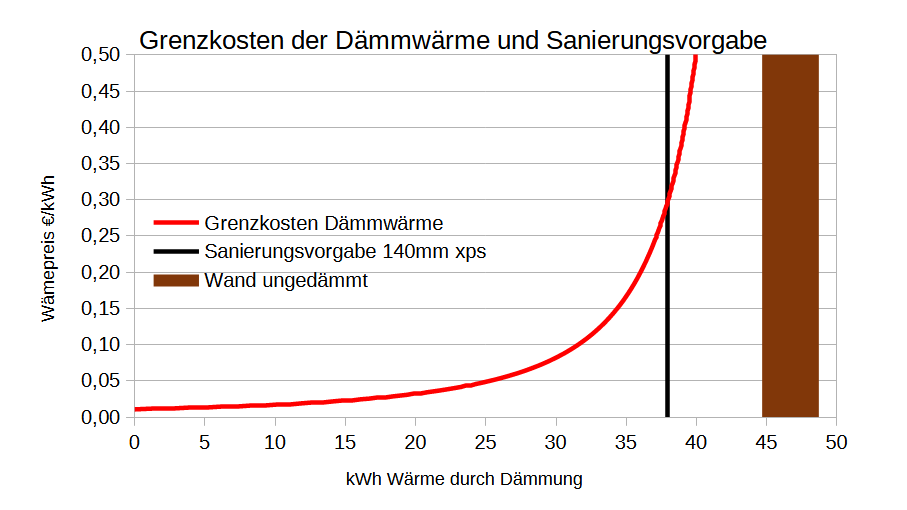
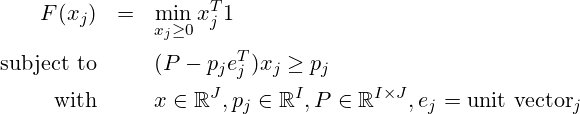Alle Jahre wieder fassen wir nach den Weihnachtstagen gute Vorsätze für das neue Jahr, vgl. Statista.

Mikrobetrachtung
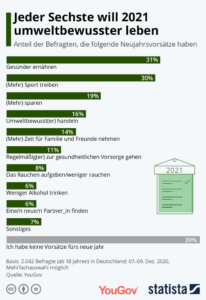
Die guten Vorsätze für 2026 von Statista gehen auf eine Befragung im Okt.-Nov. 2025 zurück, und im Folgenden werden diese zunächst als Zielvorstellung eines repräsentativen Befragten interpretiert, wobei die genannten Häufigkeiten als Zielpriorität interpretiert werden. Diese neuen Vorsätze stimmen gut mit den Vorsätzen von 2021 überein, was dann nicht gerade für die Zielerreichung spricht. Das Scheitern an den guten Vorsätzen kann man gut mit einem intrapersonellen Prinzipal-Agent-Modell erklären. Wir zerlegen unser ICH in 2 Akteure:
- Der Prinzipal repräsentiert das langfristige Selbst und definiert die guten Vorsätze, um über die gesamte Lebensspanne einen Nutzen zu erzielen. Leider ist er dabei ein bisschen „schlampig“ und betrachtet das Gefecht gerne mit Distanz vom Feldherrenhügel. Er ist aber für die reale Erfüllung der Ziele auf den Agenten angewiesen.
- Der Agent repräsentiert das kurzfristige, impulsive Selbst, das in der Gegenwart agiert. Er ist oft kurzsichtig – was man „Present Bias“ nennt – und bevorzugt sofortige Belohnung (Süßigkeiten) gegenüber langfristigen Vorteilen (Fitness). Wir Läufer können das aber auch positiv nutzen. Wir denken nicht an die noch ausstehenden 10 km, sondern konzentrieren uns auf jeden Schritt, auf die Beine, auf die Arme, auf die Atmung etc. Sieht man die Ziellinie vor sich, wirkt der „Present Bias“ wie ein Katalysator für Höchstleistungen. Geht der Agent „all in“ schmückt sich der Prinzipal später zufrieden mit Medaillen und Urkunden.
Sportlern und Läufern ist die negative Seite des Agenten auch unter dem Namen „innerer Schweinehund“ bekannt. Das gilt aber nicht nur für den Sport, sondern insbesondere auch für den Genuss. Der Prinzipal will Gesundheit in 20 Jahren, der Agent will den Zucker-Kick jetzt. Diese intrapersonellen Kräfte sind gewaltig. Um die Kräfte empirisch abzuschätzen, kann man z.B. sich mitten in einer Mahlzeit, den Teller von einer/m Bekannten unangekündigt wegziehen lassen. Der „Flow“ wird zwar nur kurz unterbrochen, aber der Agent beschwert sich augenblicklich: Unverschämtheit! Da nützen auch keine Hinweise, dass ruhiges Essen und gutes Kauen gesünder sind (Agent: Ratschläge sind auch Schläge!), da diese Argumente aus der Hemisphäre des Prinzipals kommen, vgl. auch WantingAndLiking. Wie hoch müsste die monetäre Kompensation für diese Genussbeeinträchtigung/Unverschämtheit aus Sicht des Agenten sein? 10 € oder 100 € oder 1000 €? Wenn man hier eine hohe Kompensation fordert, weiß man auch gleich, wie schwer es mit den guten Vorsätzen 2026 wird.
Hier gibt es für die meisten von uns auch Zusammenhänge zwischen Festtagsessen und Trinken, da letzteres das postprandiale Koma lindert. Beides – Essen & Trinken – buchen in die Energiegleichung mit positiven Vorzeichen. In die Komagleichung bucht Essen mit einem Plus, aber Trinken mit einem Minus (Betäubung, Lockerung). Diese beiden Gleichungen verbinden damit die Ziele „abnehmen“ und „weniger Alkohol“. Man isst weniger (Hara hachi bun me) und muss deshalb auch nicht ein folgendes Koma mit Alkohol bekämpfen. Stattdessen kann man auch „… tausend Schritte tun“ was schon mal in Richtung „mehr Sport“ geht.
Aus empirischen Untersuchungen (Prospect Theory von Kahneman und Tversky) ist die Verlustaversion bekannt: Wir gewichten Verluste etwa doppelt so stark wie Gewinne. Für den Prinzipal sind die langfristigen Gewinne ausschlaggebend: „Ich werde fit sein“. Der Agent hingegen fokussiert auf die sofortigen Verluste: Verlust an Komfort, Verlust an Zeit, Verlust an Genuss z.B. die Pizza nicht essen. Der innere Agent ist extrem risikoavers (Komfortzone: keinen Tropfen Schweiß unnötig vergießen) und wir Sportler nennen das den „inneren Schweinehund“.
Noch prekärer wird es bei physischen Anforderungen an den Agenten. Das Feldtagebuch Video zu 4 Rekrutinnen dokumentiert, wie Ausbilder der Bundeswehr versuchen, die Unterstellten auf ein geeignetes Fitnesslevel zu heben. Der Hauptfeldwebel ist hier in der Rolle des Prinzipals, die Rekrutinnen sind seine Agenten und er übt schon massiv Druck aus, um die Fitness zu steigern. Beim eigenen Vorsatz „mehr Sport“ ist mit ähnlichen intrapersonellen Widerständen zu rechnen. Ein Aspekt ist hier auch der zirkadiane Rhythmus. Jeder Läufer weiß i.d.R. ob er mehr „Lerche oder Eule“ Typ ist.
Zur artgerechten Bewegung des Menschen gehören „Gehen“ und „Laufen“, letzteres mit einer sichtbaren Flugphase. Jeder kann für sich ausprobieren, ob er 1 km ohne Pause laufen kann. I.d.R. sollte das unter 5:00min seien. Ich würde vermuten, dass das für den überwiegenden Teil der Bevölkerung unmöglich ist. „mehr Sport“ tut Not!
Nun agiert der Agent im „hier und jetzt“ häufig nicht alleine, sondern in einer Gruppe. In der Gruppe werden die gemeinsamen Aktivitäten durch Aggregation der Einzelvorstellungen gewonnen. Das sind häufig min(pi, pj, …) bzw. max(pi, pj, …) Regeln, die situativ, zeitlich oder regional unterschiedlich ausfallen können. In einer Wohlstandsgesellschaft könnte das z.B. wie folgt aussehen:
- Damit alle Personen pi einer Gruppe beim Laufen mitkommen, schreibt man jeder Person das Tempo pi=Minimum(pi, pj, …) vor. Diese Regel ist damit hinsichtlich der Aggregation das Gegenteil zum Wettkampf (🏅:Schneller, höher, stärker) und könnte auf Nietzsches Ressentiment zurückgehen. Damit fehlt beim Gruppenlauf auch die Belohnung des Wettkampfs, die dann anderweitig 🍽️&🍺erfolgen muss.
- Beim Essen hingegen darf jeder sein persönliches Maximum realisieren. Man duldet keine Bevormundung hinsichtlich Tempo (Unverschämtheit!), Menge (Frechheit!) und Zusammensetzung (Ratschläge sind auch Schläge!). Im Gegenteil beäugt man diejenigen kritisch, die offensichtlich unter ihrem hedonistischen Maximum bleiben (Genussverweigerer!).
Einerseits fallen diese Aggregationen (min, max) in Kriegsgebieten und Krisenzeiten offensichtlich anders aus (der Schnellste bekommt Alles), andererseits sind sie vermutlich für die Verbreitung von Wohlstandskrankheiten wie Übergewicht etc. maßgeblich. Die Framingham Heart Study unterstreicht die Bedeutung von Gruppen und sozialen Netzwerken für die Verbreitung von Übergewicht. Neben den sozialen Faktoren schaffen aber auch abiotische Faktoren (Wohnung, Siedlung, Verkehr) ein adipogenes Habitat. Diese Mechanismen führen in Summe zu erheblichen Kosten im Gesundheitssystem. Die World Obesity Federation schätzt die Kosten für Übergewicht auf ca. 114 Mrd. USD/Jahr in Deutschland im Jahr 2025. Wenn Länder wie die 🇺🇸 USA, diese Kosten bei der Einreise berücksichtigen, kann das in 🇩🇪 zu einer adversen Selektion und Ausweitung der VFL führen.
Für den intrapersonellen Agenten der Wohlstandsgesellschaft sind diese Aggregationsregeln „ein gefundenes Fressen“, was zum Moral Hazard führt. Das Scheitern des sozialen Umfelds dient als Legitimationsquelle für das Scheitern des Agenten gegenüber seinem Prinzipal: die Anderen lassen sich ja auch gehen. Umgekehrt sieht es der gescheiterte Agent nicht gerne, wenn andere Agenten ihr Ziel erreichen, weil es ihm die Argumentation gegenüber seinem eigenen Prinzipal erschwert und zu maliziösem Neid führt, vgl. Nietzsches Sklavenmoral. Man kann das als kognitive Dissonanz zwischen Prinzipal und Agent auffassen. Um das Selbstwertgefühl des Prinzipals zu schützen und ihn vor Ohnmacht zu bewahren, wird das Andere verteufelt (Nietzsches „böse“) und die Unzulänglichkeiten des Agenten (Hedonismus) zu „gut“ umgewertet. Diese neue Moral breitet sich bis in die Köpfe der politischen und wirtschaftlichen Eliten aus mit dem Ergebnis, dass z.B. ab 2026 der Leistungskatolg der GKV um Fettabsaugung erweitert wird. Meine Erfahrung ist, dass diese Muster mehr die Regel als die Ausnahme in unserer Gesellschaft sind. Das olympische Motto „Höher“,“Schneller“, „Weiter“ hat in dieser Moral eine negative Konnotation, mit „All You Can Eat“ wird geworben.
Im größeren Gruppenzusammenhang lauert die Gefahr der falschen Propheten mit Meinungsführerschaft:
- Sie führen Helmut Schmidt (97 Jahre) an, um das Rauchen zu relativieren.
- Sie verweisen mit „No Sports“ auf Winston Churchill (90 Jahre) um die eigene Faulheit zu rechtfertigen. Gelegentlich wird das dann zur Sportsucht – der man nicht verfallen darf – überhöht.
- Sie sprechen von mediterraner Ernährung, meinen aber Pizza+Rotwein+Grappa.
- Sie sprechen täglichem Alkoholkonsum in Form von Rotwein gesundheitsförderliche Wirkung zu: drink doch ene met, stell disch net esu ann.
- Sie sprechen von Vitamin B12 und Eisen, aber eigentlich geht es um Currywurst Rot-Weiss + Cola oder Nackenkotelett+Bier.
- Sie sprechen von Naschkatzen und verniedlichen den übermäßigen Zuckerkonsum.
- Sie sprechen von abwechslungsreichem Essen, meinen aber eine Endlositeration zwischen Twix, Mars, Snickers, Milka, Nutella etc.
- Sie sprechen über die Gefahren der Magersucht, übersehen aber die eigene Plauze.
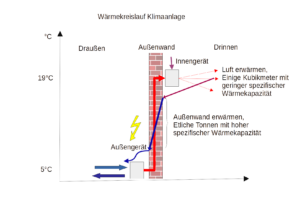
Die Botschaften der falschen Propheten nimmt der intrapersonelle Agent gerne auf und leitet für sich daraus das Habitat „Komfortzone“ als artgerechten Lebensraum ab, leider mit fatalen Konsequenzen, wenn er dem Jahrzehnte folgt. Häufig ist in den irreführenden Aussagen ein Funke Wahrheit enthalten, aber für das Gesamtbild sind sie nur von untergeordneter Bedeutung, vgl. DKV-Report2025. Man erkennt den falschen Propheten häufig an den Auslassungen, also das was er nicht sagt. Die Follower neigen dazu, sich das Habitat gemäß der Genussanforderungen einzurichten (großer Kühlschrank, Fritteuse, ultra wide monitor und natürlich die Couch), so dass keine Wünsche offen bleiben, was aber mit dem Ziel „sparen“ kollidiert. Da der Verlust des Habitats durch „ich laufe jetzt“ doppelt wiegt (Verlustaversion), macht man es sich selber schwer mit „mehr Sport“. Man kann das z.B. mildern, in dem man die Zimmertemperatur auf 19°C zurückfährt und so auch „mehr für die Umwelt“ tut.
Aber auch der intrapersonelle Prinzipal hat in der Zielformulierung seine Unzulänglichkeiten. Häufig entstehen seine guten Vorsätze aus einem Silo-Denken wie z.B. Gesundheit, Familie, Job, Genuss etc. weil er vom Feldherrenhügel nur grob die Strukturen erkennt und die Verbindungen übersieht. Aus der Politik ist uns das bekannt (Haushalt für Verteidigung, Soziales), aber wir haben auch Zielinkonsistenzen bei unseren guten Vorsätzen.
Nehmen wir an, der Prinzipal formuliert Ziele a und b – von denen er mehr erreichen will – als gute Vorsätze. Er übersieht – vorsätzlich oder schlampig – dann externe gerne Regeln der Form a+b ≤ Konstant bzw. p(a+b ≤ Konstant) >0,95. Wie passen die Ziele („mehr Geld sparen“, „bessere Leistung im Job“, „weniger Stress im Büro“,“mehr Zeit für Familie“, „mehr Sport“) zusammen? Offensichtlich fehlen hier Zeit und Geld Restriktion. Ein kluger Prinzipal plant nicht gegen die Mathematik, sondern mit ihr. Dafür muss man aber die externen Regeln/Restriktionen identifizieren, substitutive und komplementäre Ziele erkennen und benennen. („Gesünder ernähren“, „mehr Sport“, „Abnehmen“, „weniger Alkohol“) wären nach meiner Einschätzung komplementäre Ziele, die sich gegenseitig verstärken, während das zuvor genannte Ziel-Tupel eher substitutiv ist: Man kann sie mit großer Wahrscheinlichkeit nicht gleichzeitig erreichen. Der Prinzipal muss dann in Hinblick auf den Agenten überlegen, in welchem sozialen Umfeld der Agent die Ziele des Prinzipals mit erträglichem „murren“ umsetzen kann. Denn sonst braucht es den rauen Ton aus dem Feldtagebuch, um die Ziele zu erreichen. Und wer tut sich das schon freiwillig in seiner Freizeit an?
- Man sollte die inneren Widerstände und Ausreden nicht unterschätzen, die sich aus der kurzfristigen Sicht des Agenten ergeben. Überschätze Dich nicht, mache es Deinem Agenten nicht unnötig schwer und nutze den „Present Bias“ z.B. im Sport für Dich.
- Man muss alle relevanten Restriktionen wie z.B. Geld, Zeit,Konventionen etc. detailliert in den Plan aufnehmen, sonst ist das Scheitern wahrscheinlich.
- Man sollte komplementäre und substitutive Ziele erkennen, und sich im Zweifel für ein Bündel komplementärer Ziele entscheiden.
- Man sollte sich für eine förderliche Sozialumgebung (incl. Aggregationsregel) entscheiden und die, die das Festhalten am „Way of Life“ predigen und Änderungen verteufeln, kritisch zu Kenntnis nehmen. Du kannst Sie wie ein Satellit ewig umkreisen, wenn Du nicht ihrer Schwerkraft folgst. Diese Kraft nimmt reziprok mit dem Abstand ab.
Makrobetrachtung
Alternativ kann man die Häufigkeiten als Zielvorstellungen mehrerer Personen auffassen, wobei es auch da Überschneidungen geben muss (Mehrfachauswahl war möglich), da die Summe der relativen Häufigkeiten > 1 ist. Ein Nichtraucher – das sind derzeit ca. 80% der Bevölkerung – wird sich für 2026 nicht vornehmen „mit dem Rauchen aufzuhören“ = 15% in der Umfrage. Dies vorausgesetzt, nehmen sich ca. 75% der Raucher vor, das Rauchen zu beenden. Die Vorstellung, dass das der Masse (>50%) aller Raucher gelingt, ist illusorisch. Ähnlich verhält es sich vermutlich mit dem Wunsch „Abnehmen“=37%, wobei ca. 60% übergewichtig (53% Frauen, 67% Männer) sind. Wenn man auch hier wieder annimmt, dass nur Personen mit dem Risikomerkmal Übergewicht sich vornehmen abzunehmen, sind das ca. 60% der Betroffenen. Auch hier ist die Zielerreichung fraglich, zumal der zeitliche Trend auch dagegen spricht.
Würden die guten Vorsätze 2026 flächendeckend in Deutschland umgesetzt, wäre das für unsere Wirtschaft und Gemeinwesen (Sozialversicherungen, öffentliche Hand) von erheblicher Bedeutung.
Wenn man das Ziel „mehr sparen“ verfolgt, kann das auch ein Beitrag zur privaten Altersvorsorge sein. Im Gegenzug nimmt die Konsumnachfrage ab. Händler (Umsatz) und öffentliche Hand (Mehrwertsteuer) verlieren also, Finanzdienstleister (Banken & Versicherungen) werden vermutlich profitieren.
„Abnehmen“, „gesünder Ernähren“, „Sport“, „weniger Alkohol“ & „rauchen aufhören“ sind sicherlich Ziele, die die gesetzliche und private Krankenversicherung (KV) erheblich in ihren Leistungen entlasten würde, vgl. die oben zitierten 114 Mrd. USD/Jahr (bei 66 Mio. Beitragszahlern entspricht das 140€/Monat) und den DKV-Report2025. Dies würde die Beitragsdynamik bei der KV stoppen und den Produktionsfaktor Arbeit und die mit ihr erstellten inländischen Produkte konkurrenzfähiger gegenüber Importen bzw. auf den Weltmärkten machen. Ebenfalls dürfte der Krankenstand bei den Unternehmen deutlich zurückgehen. Die aktuelle Diskussion über mehr Arbeit durch Feiertagskürzung, Karenztage, Praxisgebühr, Renteneintrittsalter etc. könnte deutlich entschärft werden. Gesundheitsökonomen sind sich einig, dass Prävention für den Patienten als auch für Wirtschaft und Gemeinwesen deutlich günstiger ist, als leidvolle und teure Eingriffe durch die Medizin.
Aber wie wäre die öffentliche Hand von der Umsetzung dieser Gesundheitsziele betroffen? Die Umsetzung von „abnehmen“, „weniger Alkohol“ und „rauchen aufhören“ würden zunächst große Haushaltslöcher erzeugen (Mehrwertsteuer, Alkoholsteuer, Tabaksteuer). Die Wertschöpfung im Gesundheitssektor und die damit verbundenen Steuereinnahmen (Mehrwertsteuer, Einkommenssteuer) würden ebenfalls zurückgehen, weil Prävention kostengünstiger ist als Krankheitsbehandlung. Die gesunkenen Kosten der KV kämen den Beitragszahlern und Arbeitgebern zugute, weniger der öffentlichen Hand. Gesünder leben bedeutet i.d.R. auch höhere Lebenserwartung („rauchen aufhören“ = ca. +5 Jahre Rentenbezug mehr), was perspektivisch die Zuschüsse aus dem Bundeshaushalt zur Rentenversicherung erhöhen wird, also ein weiteres Minus für den Haushalt. Aus Sicht der öffentlichen Haushalte müsste man eine „gute Vorsatz“-Welle 2026 eher fürchten als begrüßen. Vermutlich ist das der Elefant im Raum, den keiner sieht. Stattdessen wird Zwist und Zwietracht gesät (Beitragsbemessungsgrenze, Praxisgebühr, ambulant versus stationär, Verwaltungsebenen, etc.) und den beteiligten Wirtschaftseinheiten die Augen verbunden, mit dem Effekt: Wenn zwei sich streiten, freut sich der Dritte, der sich mit dem Zwist profilieren kann, was ihm insbesondere vor dem Hintergrund der Landtagswahlen 2026 wichtig ist. Dieses Parteiverhalten führt zum beobachteten Erstarken der politischen Ränder und lässt sich aus dem Gefangenendilemma erklären. Verlierer ist die kollektive Rationalität: Prävention ist besser als Heilen und erspart vielen das Leiden.
Um die guten Vorsätze zu fördern, würde ich deshalb mehr auf Marktmechanismen setzen, die die externen Effekte der guten Vorsätze in die Gesundheitspreise bringen (Bei CO2 Emissionen oder Tabak machen wir das ja auch im Mrd. € Bereich mit Pigout Steuern oder property rights). Gesundheit muss sich hier & jetzt lohnen und nicht erst in 20 Jahren, soviel Geduld kann man nicht voraussetzen. Bei der Krankenversicherung wären das Bonus/Malus Systeme, XXL-Tarife, Selbstbehalt etc., mit dem Ziel, die Entstehung und Behandlung von Wohlstandskrankheiten der eigenen (!) Versicherten zu senken. Die Überlegungen aus dem Prinzipal-Agenten-Modell für den Versicherten haben deutlich gemacht, dass für Genussbeeinträchtigungen wie z.B. „abnehmen“, „weniger Alkohol“ & „Sport“ schon erhebliche Kompensationszahlungen nötig sind, bis dieser sein Verhalten ändert. 1 €/Tag wird daran wahrscheinlich nichts nachhaltig ändern. Es müssten vermutlich schon – wie bei Tabak – 6 €/Tag sein.