Abstract
In this paper I analyze the intermediate and finishing times of male runners over several years in a marathon. Surprisingly the age group M40 performs best, leading to a U shaped curvature for age groups. The distribution of intermediate and finishing times seems to be bimodal with peaks at 3:30 and 4:00 hours, which might be an effect of guidance by popular “pacemaker”. The average split relation between second and first part of the marathon for runners, who do not increase the pace in the second part was found to be 1.10. The solutions for the 50% quantile regression, suggests a surcharge of 3% up to 5% which should be best for finishing times in the range of 3:00 to 4:30 hours.
In the last part, I try to remove the age effect from the finishing times by preserving the empirical distributions in each age group. I argue that the resulting age adjusted times are equal to the age graded times. This implies different age grading factors for the quantiles of finishing times, which are reasonable from a physiological point of view. The age grading factors are estimated by a parametric quantile regression and are compared with the WMA gradings. For the lower quantiles, the WMA gradings are in the range of the estimated 3% an 10% quantile. For the midrange quantiles of runners, the WMA gradings seems to overestimate the age effect because the age degression in this category was found to be much lower than in the estimated world best times from WMA.
Altersabhängige Leistung
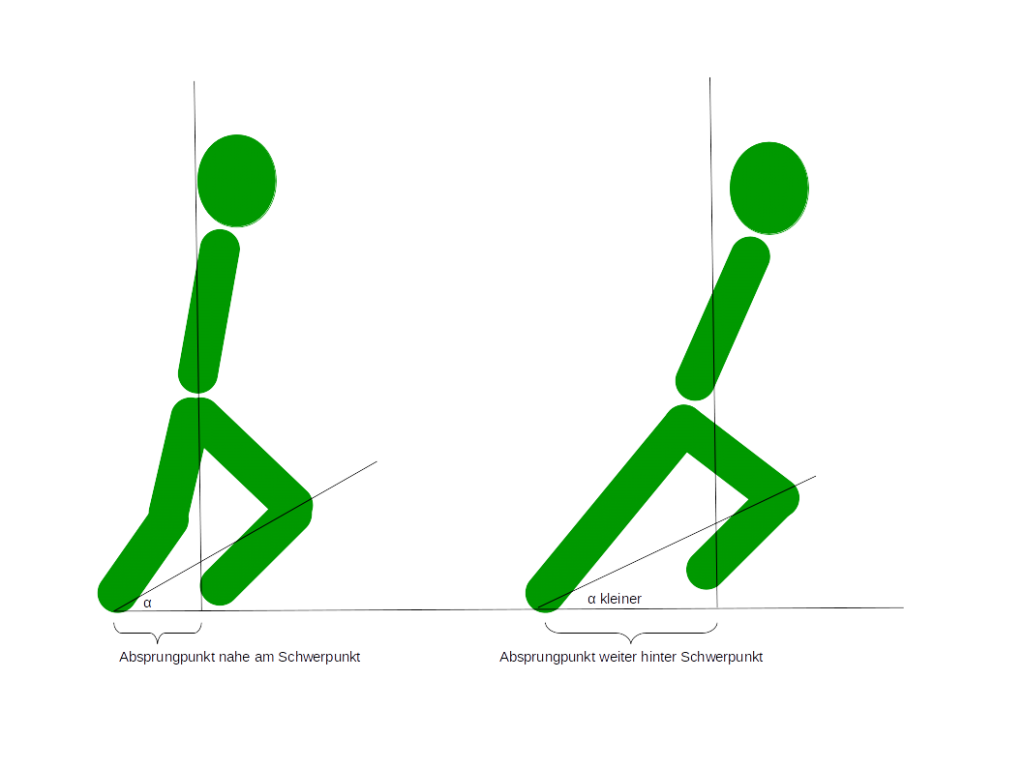
Unsere sportlichen Leistungen sind sicherlich vor dem Hintergrund des Sportleralters (a) zu sehen und wir schauen uns nach Wettkämpfen zur eigenen Positionsbestimmung gerne die Einstufung nach den Altersklassen des DLV an. Nach den Darstellungen zur Laufleistung P [W], gibt es folgenden Zusammenhang zwischen der dominierenden Hubleistung P und der Zeit (t) für eine gegebene Strecke (s).
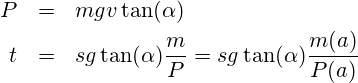
Nach Angaben des statistischen Bundesamt nimmt die mittlere Körpermasse bei Männern bis zu einem Alter von 60 zu. Dieser Trend – sicherlich nicht in allen Teilen einer Naturgesetzmäßigkeit sondern eher dem Wohlstand geschuldet – dürfte an der Masse der Freizeitläufer nicht vorbeigehen.
Des Weiteren dürfte die Leistungsfähigkeit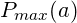 
mit dem Alter ab 25-30 Jahre aufgrund physiologischer Änderungen und abnehmender Muskelmasse (vgl. loges) ebenfalls zurück gehen. Der allgemeine Gewichtstrend besteht damit wahrscheinlich eher in einer Zunahme von Körperfett, was beim Laufen zu linearen Zuschlägen bei der Endzeit führt.
Es gibt also einige Gründe für das anwachsen des Bruchs m(a)/P(a) mit zunehmendem Alter a und daraus resultieren dann schlechtere Zeiten t für eine Strecke s.
- Durch den skizzierten Alterszusammenhang wird eher die maximale Leistungsfähigkeit und nicht die real mögliche Leistung beschrieben. Insofern dürften Läufer, die an ihrer Leistungsgrenze
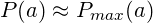laufen davon stärker tangiert sein, als Freizeitläufer mit moderatem Tempo die ihr Leistungspotential 
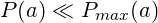nicht ausschöpfen. Diese Zurückhaltung kann einerseits mit der Motivation und Zielsetzung (Dabei sein ist alles!) andererseits mit der Unkenntnis der eigenen Leistungsfähigkeit (Kann ich das Tempo halten?) zusammen hängen.
- Diese Argumentation gilt zunächst nur im Mittel d.h. für den Erwartungswert E[m(a)/P(a)] und es gibt viele Möglichkeiten – nicht zuletzt das Laufen selber – diesem allgemeinen Trend durch Technik, Training und leistungsgerechter Ernährung entgegenzuwirken. Die Bestleistungen der WMA belegen eindrucksvoll die Leistungsfähigkeit im Alter. Von diesen biologischen Grenzen dürften 99% der Freizeitläufer – mich eingeschlossen – meilenweit entfernt sein. Für den Rest der Bevölkerung – ohne alltäglichen Sport – sind diese Altersleistungen schon unfassbar, und selbst wir Freizeitläufer sehen uns häufig einer Kritik ausgesetzt, die vermutlich mehr dem schlechten Gewissen der Untätigen geschuldet ist, vgl. Steffny.
Marathon Zeitverteilungen
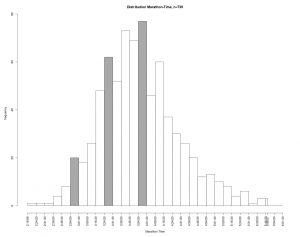
Einen ersten Eindruck zur Variation bei Läufern liefern die publizierten Tabellen zu Marathon Finisher Zeiten nach Altersklassen. Dazu werden die Ergebnisse mehrerer Jahre von einem flachen Marathon (überwiegend asphaltiert) gepoolt und für Männer statistisch ausgewertet.
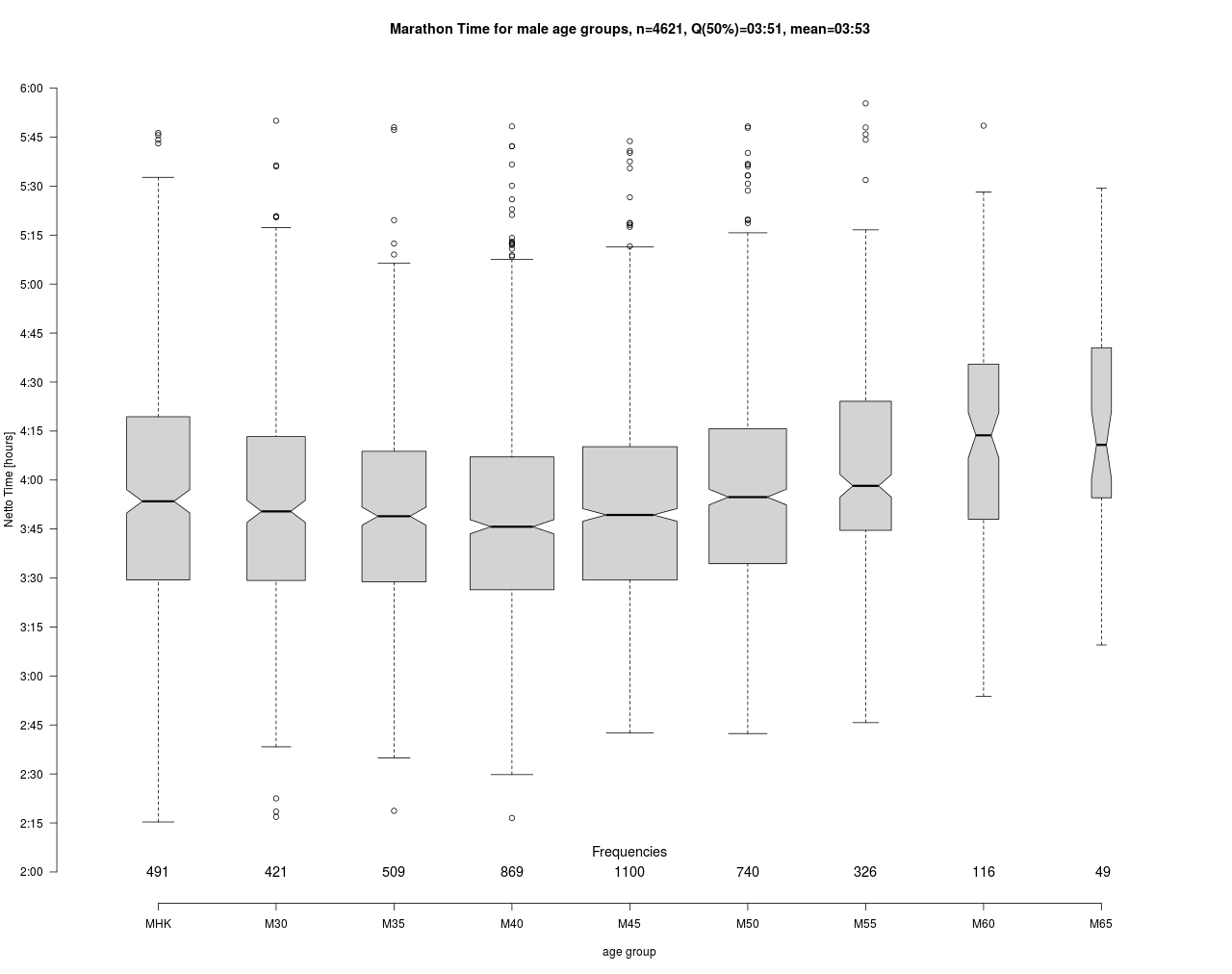
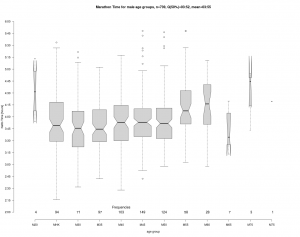
In die Auswertung sind ca. 4600 Finisher Zeiten eingegangen. 50% der Läufer erreichten das Ziel vor 3:51 Stunden. Der Mittelwert mit 3:53 liegt in Nähe des Medians und ist verglichen mit den in Durchschnitte genannten Zeit von 4:29.52 deutlich niedriger. An der Breite der Boxes im Boxplot sowie an den unten genannten Häufigkeiten erkennt man, dass die AK 40, 45 und 50 am stärksten besetzt sind und ca. 60% aller Teilnehmer stellen. Dies könnte dem demographischen Aufbau (Baby-Boomer) geschuldet sein.
Überraschend ist der Verlauf der Mittelwerte in Abhängigkeit der Altersklassen. Zwar werden erwartungsgemäß in der jüngsten Klasse MHK auch die besten Zeiten gelaufen (unterer Whisker MHK), für die Masse der Läufer sieht es aber anders aus. Demnach erreichen diese erst mit 40 Jahren im Mittel (genau genommen Median) ihr Minimum und erst danach geht es stetig bergauf mit den Marathonzeiten bis zur Altersklasse M60. Im Mittel sind also die Jüngeren nicht schneller als die midlife Läufer. Da sich die Kerben (notches) von MHK und M40 in der Grafik nicht überschneiden, kann man vermuten, dass der Unterschied signifikant ist d.h. die AK40 im Mittel schneller ist als die MHK.
Mit einem Tukey HSD Test wird untersucht, ob die Differenzen in den Altersklassen-Mittelwerten signifikant sind.
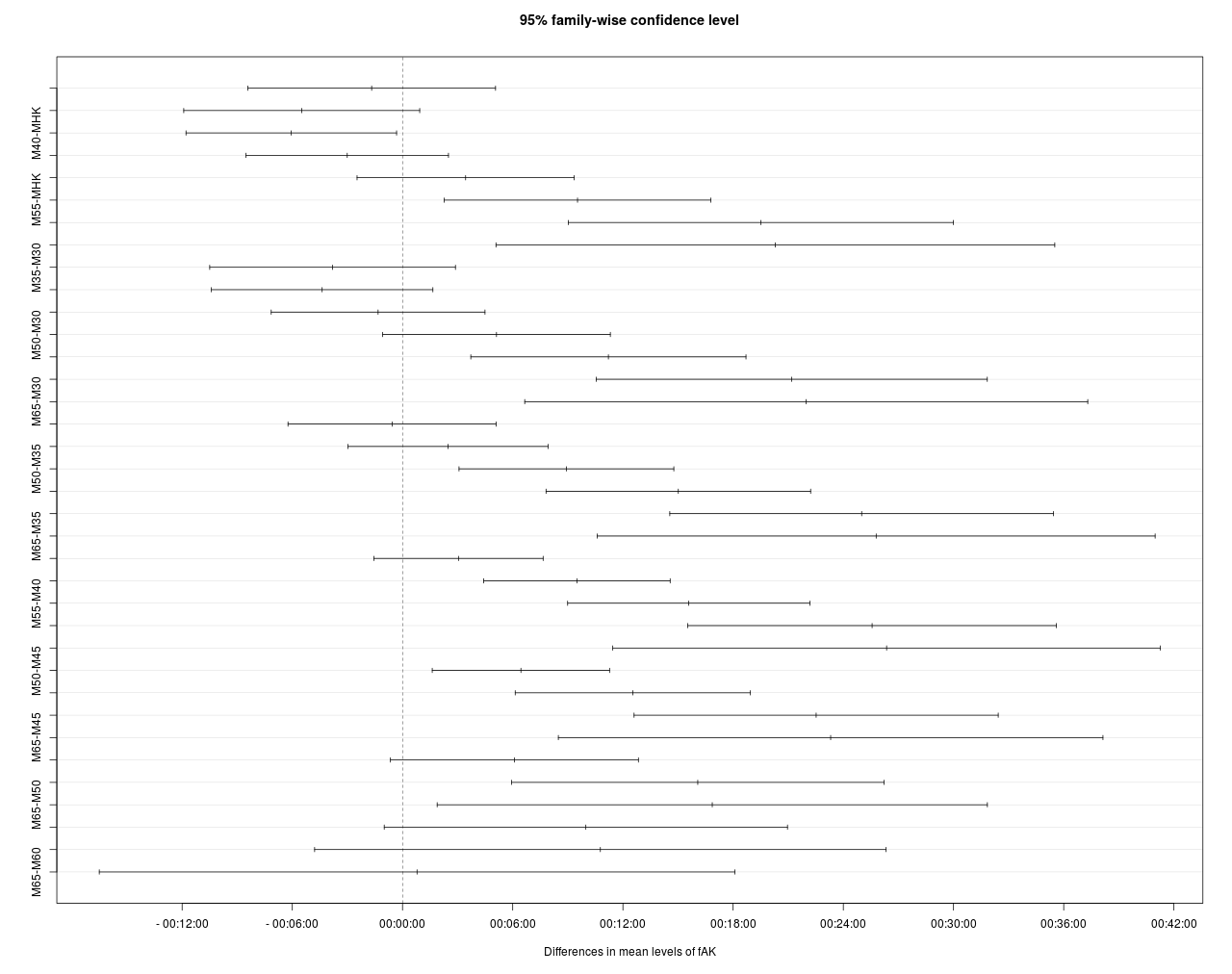
Demnach enthält das Konfidenzintervall von MHK – M45 die 0:00 und hat somit keinen signifikanten Einfluss (obere Balkengruppe mit 8 Elementen). Gleiches gilt für den Vergleich MHK – M50. Beim Vergleich mit M40 schneiden sogar die älteren Läufer signifikant besser ab.
Der Vergleich der Mittelwerte, führt hier zu weniger „intuitiven“ Ergebnissen, da die MHK die Topläufer stellt und diese Topleistungen mit M50 schon aus physiologischen Überlegungen nicht mehr erreichbar sind. Die MHK besteht aber eben nicht nur aus externen, angereisten Topläufern die dem Ruf des Preisgelds gefolgt sind, sondern auch aus MHK Freizeitläufer und diese sorgen hier für die Varianz in der Gruppe, so dass diese ihre Sonderstellung verliert. Eine Untersuchung mit ähnlicher Fragestellung findet man in Connick_Beckman_Tweedy.
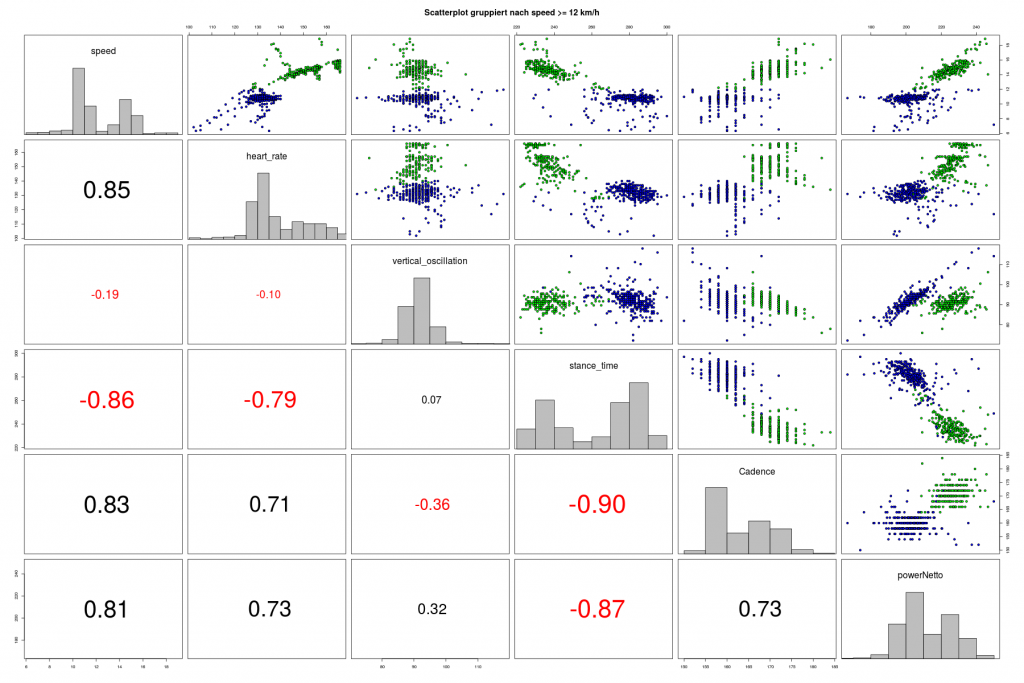
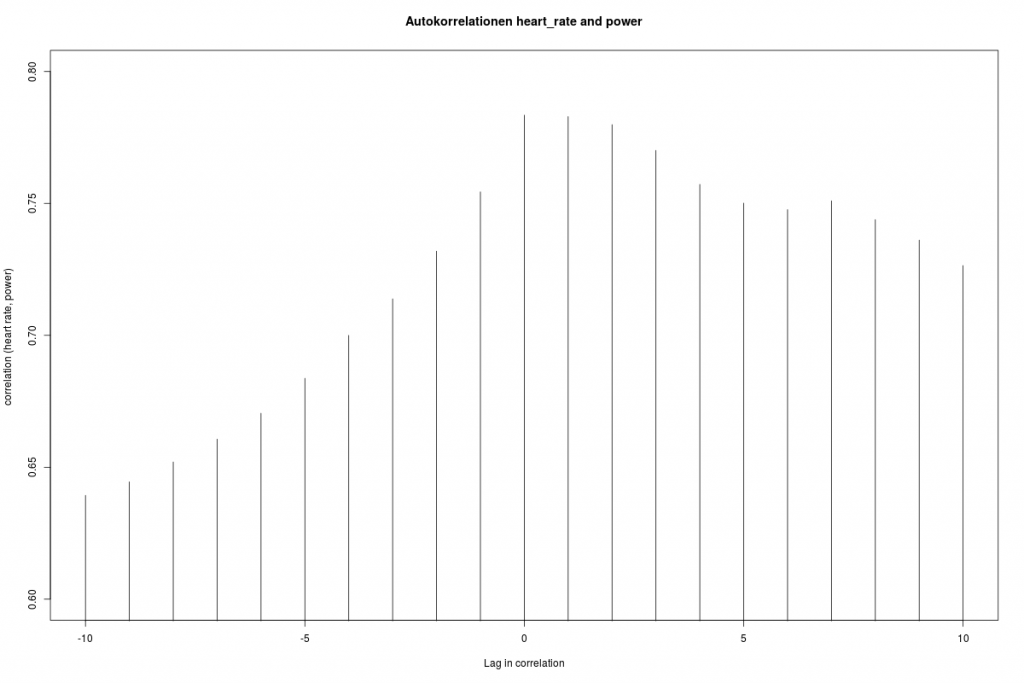
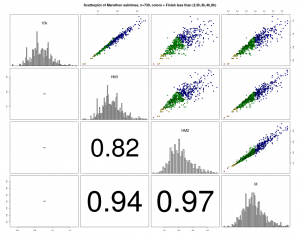
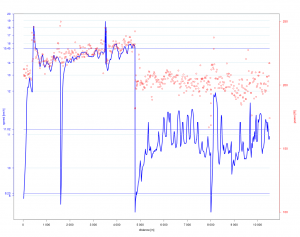
Zu diesem Marathon liegen neben den Finisher-Zeiten auch Zwischenzeiten vor die im folgenden Scatterplot dargestellt sind.
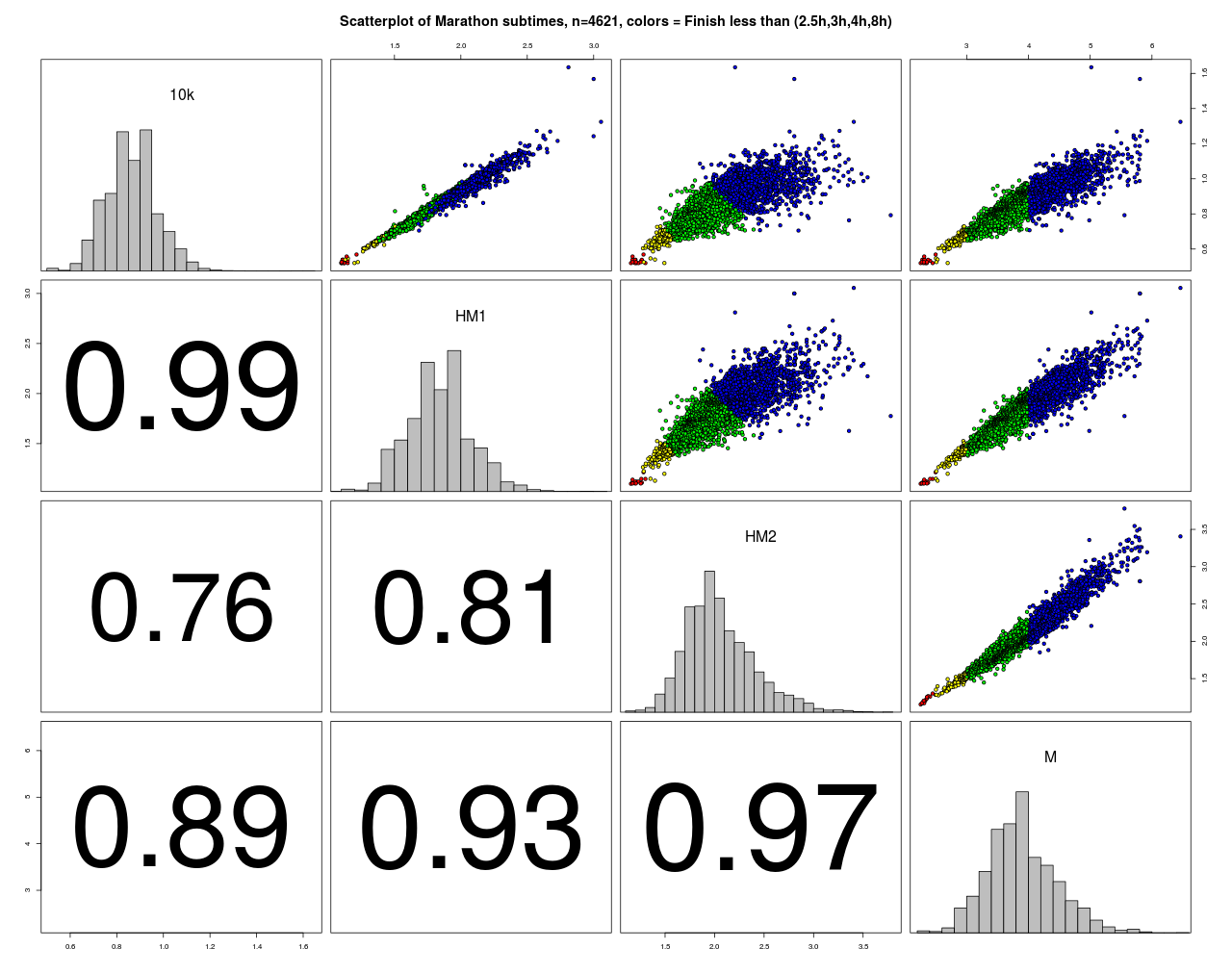
Die Farben der Punkte sind hier nach der Endzeit vergeben. Alle Korrelationen sind sehr hoch und je näher die Streckenabschnitte zusammen liegen, desto höher sind sie. Den größten Einfluss auf das Ergebnis hat erwartungsgemäß die 2. Laufhälfte. Auffällig ist, dass mit zunehmender Endzeit, die Varianz in den Vorzeiten zunimmt. Man kann also eine größere Endzeit mit verschiedenen Aufteilungen in Zwischenzeiten erreichen („Viele Wege führen nach Rom“). Für die Spitzenzeiten gilt das natürlich nicht.
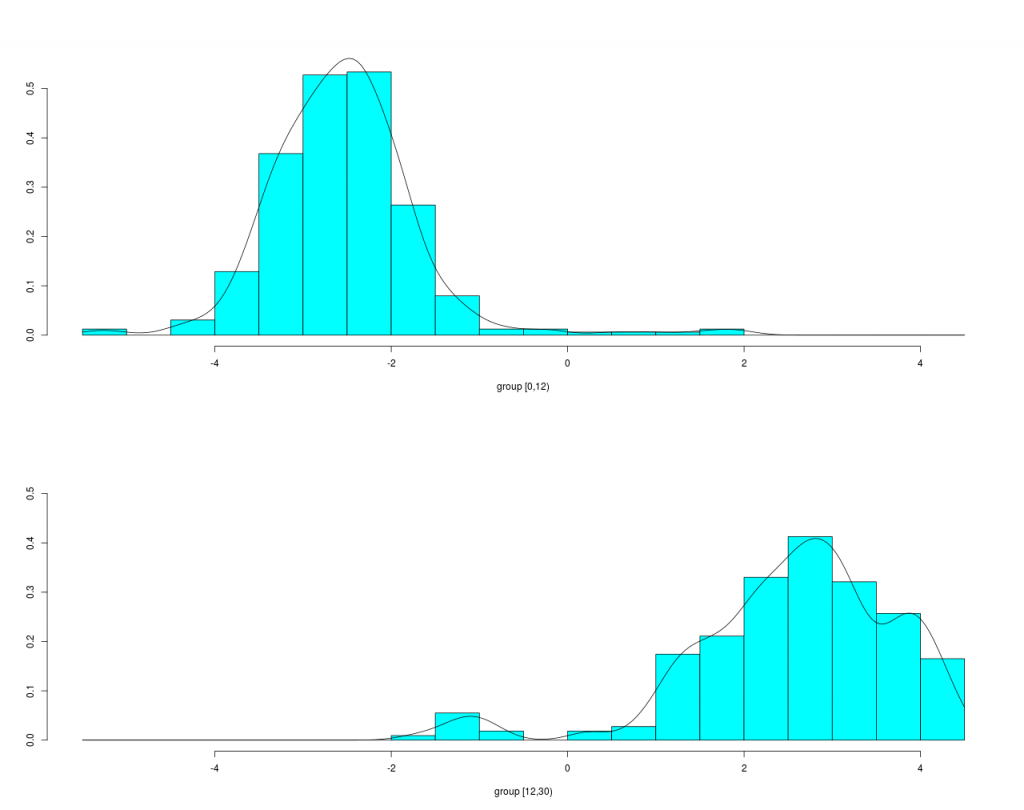
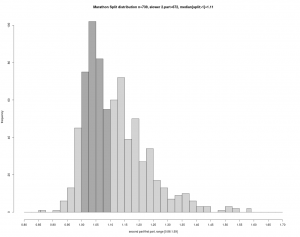
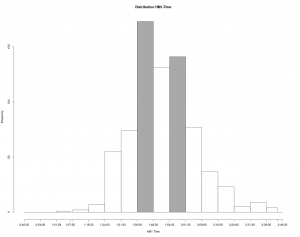
Die Verteilung der HM1-Zeiten sind im Folgenden noch mal detaillierter dargestellt.
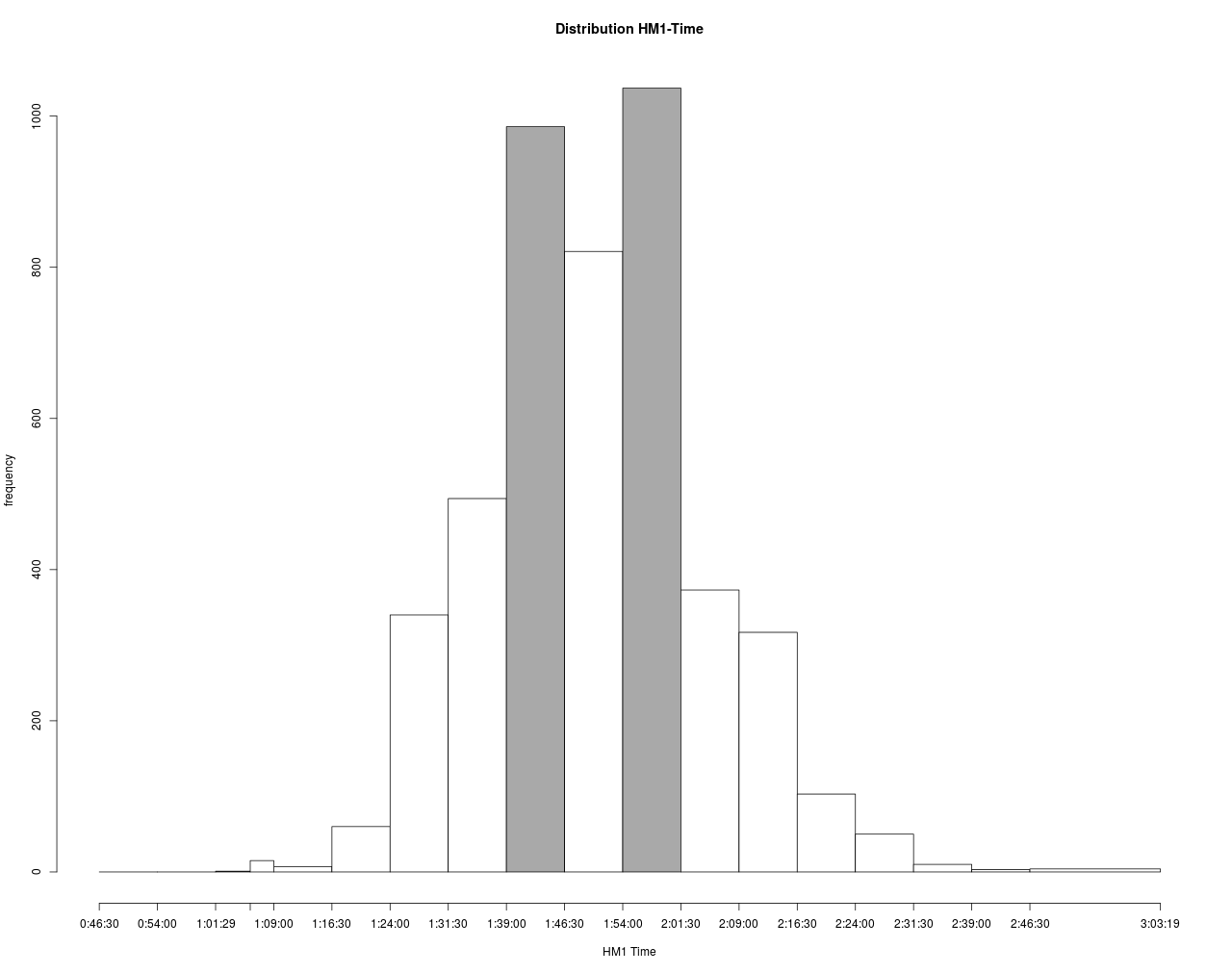
Hier erkennt man zwei Häufungspunkte bei ca. 1:40 und 2:00 Stunden. Dies wird sehr wahrscheinlich mit der Zielsetzung der Läufer, den Marathon mit 3:30 oder 4:00 abzuschließen, verbunden sein. Weiterhin gibt es Zug- und Bremsläufer mit damit assoziierten Zielzeiten. Wenn man solche Zeiten als Ergebnis eines stochastischen Prozess betrachtet, dann kommt die Stochastik hier aus einer mindestens zweigipfliegen Verteilung. Die Zug- und Bremsläufer haben also erkennbare Spuren hinterlassen, was ja auch der Zielsetzung entspricht.
Diese 2 Gipfel in der HM1-Verteilung können sich – in leicht abgeschwächter Form – ins Ziel retten.
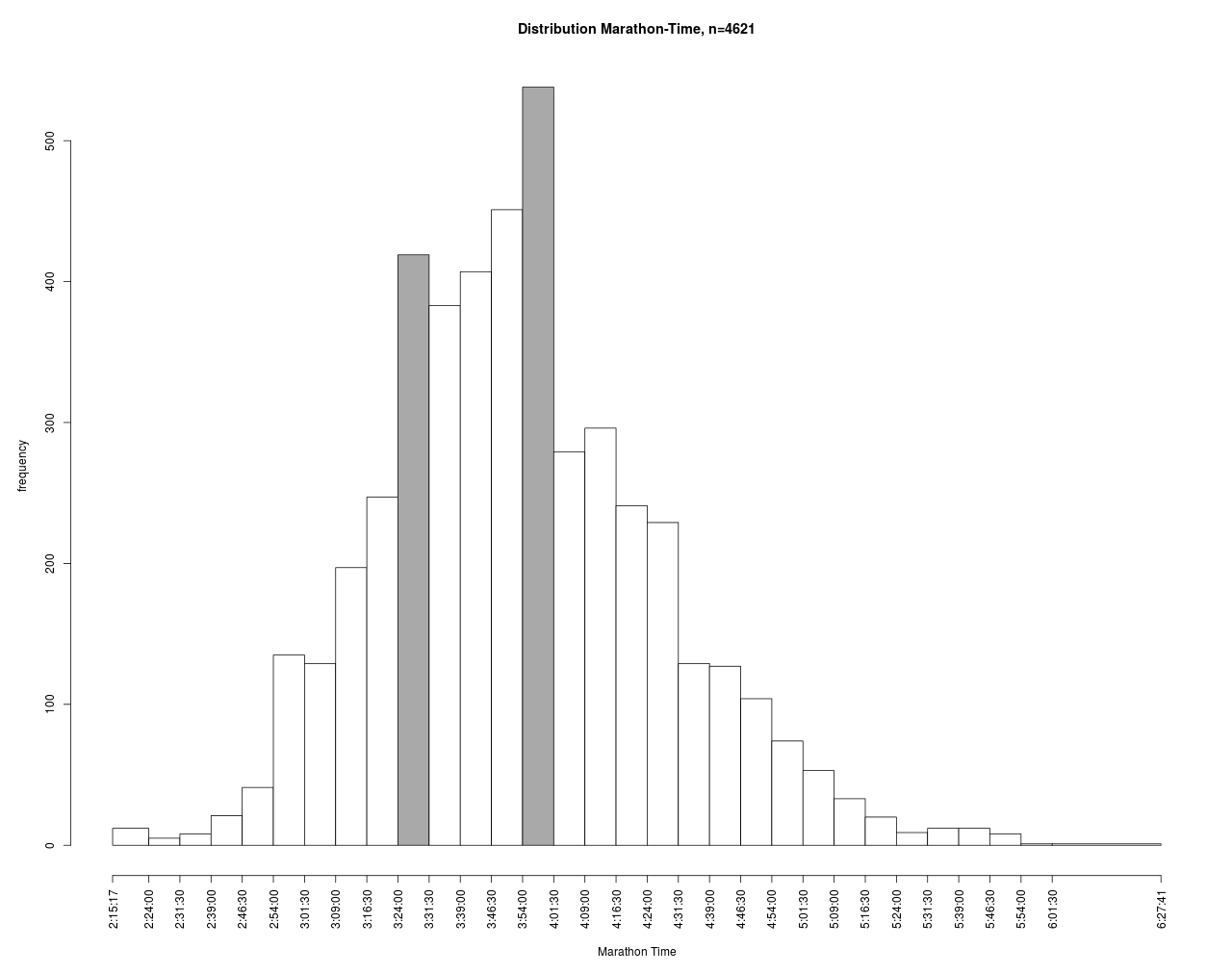
Weiterhin spricht auch dieser Umstand dafür, dass die meisten Läufer nicht an ihrer persönlichen Leistungsgrenze laufen, da sonst die Häufungspunkte wahrscheinlich nicht so deutlich entstehen würden. Man könnte entgegnen, dass diese Häufungspunkte durch die Zusammensetzung der Läuferschaft entstanden sind. Dies dürfte aber sehr unwahrscheinlich sein, da es aus physiologischer Sicht keinen Hinweis auf Mehrgipfligkeit gibt und das Alters-spektrum (vgl. Boxplot) recht kontinuierlich aufgebaut ist.
Inverser Split?
Im Zusammenhang mit der Zielzeit ist die Aufteilung der Zeit auf die beiden Laufhälften ein heftig diskutiertes Thema in der Läuferschaft. Man spricht von einem inversen Split, wenn die 2. Hälfte schneller als die Erste gelaufen wird.
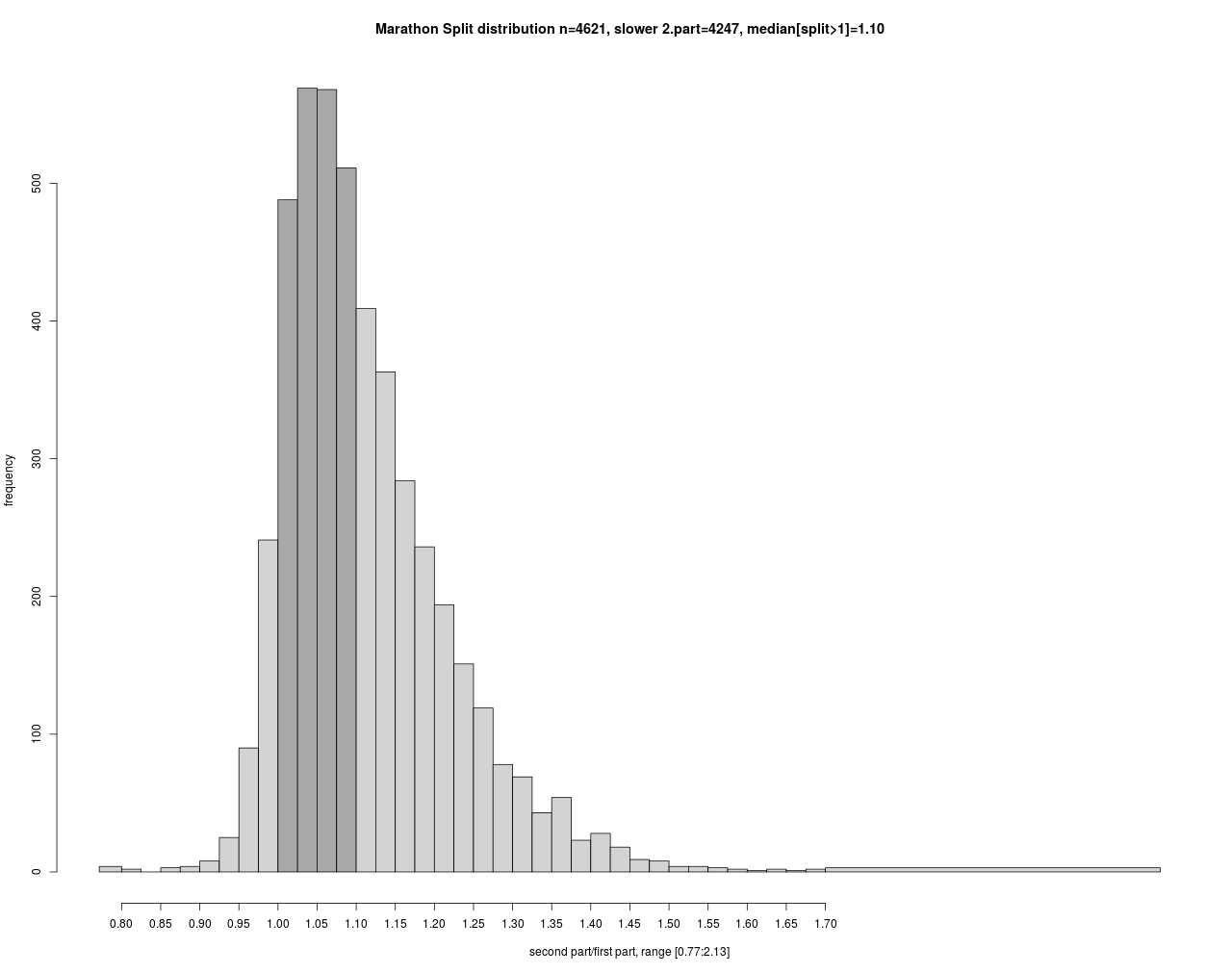
Den meisten Läufern gelingt aber kein inverser Split. Diese laufen die zweite Hälfte ca. 10% langsamer als die erste. Auf beide Hälften bezogen bedeutet dies einen Zuschlag von 5% zur Halbmarathonzeit.
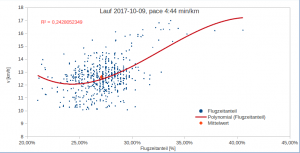
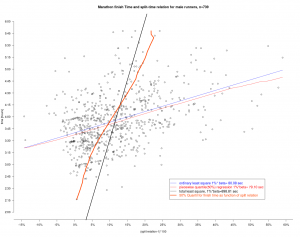
Wie hängen nun Split-Relation und Finishtime zusammen? Dazu wurden verschiedene Modelle angesetzt.
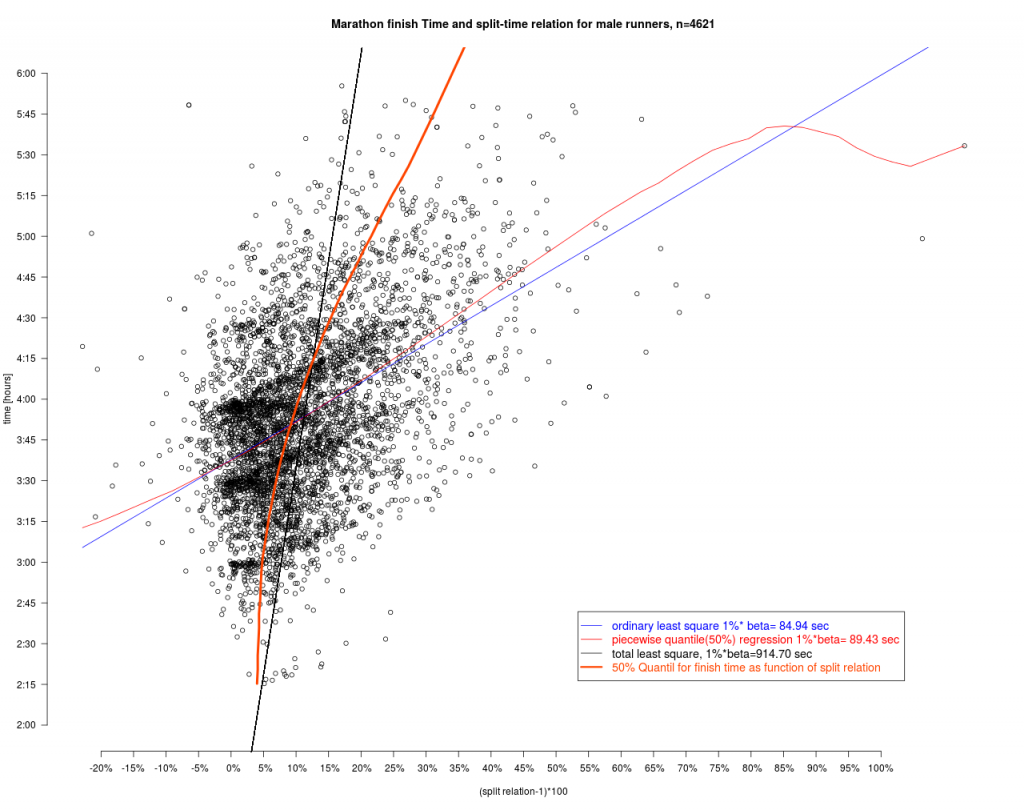
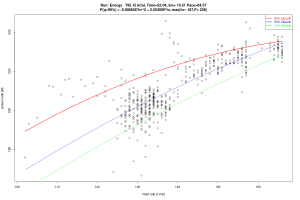
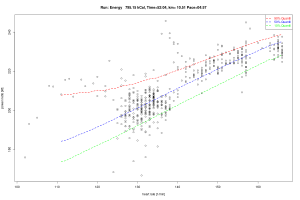
Dieser Grafik entnimmt man, das jeder Prozentpunkt mehr in der Splitrelation zu spürbaren Zuschlägen in der Endzeit führen. Das Total least squares führt hier zu den größten Zuschlägen. Für die Interpretation der TLS Geraden geht man wie folgt vor: Man nimmt einen Punkt – z.B. die eigene Laufleistung – und fällt von diesem das Lot auf die TLS Gerade und erhält so den Schätzwert und 2 Residuen. Dem TLS Ansatz liegt die Vorstellung zu Grunde, dass beide Werte – finish und split – durch zufällige Ereignisse geprägt sind, während bei der Standardregression der Fehler nur in der abhängigen (hier finish) auftritt. Dies kann hier aber durchaus bezweifelt werden.
Bei dem 50% Quantilt für die Finishtime als Funktion der splitrelation ist die Fragestellung andersherum: Gegeben ist hier die Zielzeit und diese Linie gibt dann die 50% Grenze für den split an. Beispiel: Möchte man 3:00 Stunden laufen, so sollte der Zuschlag 3% für die zweite Hälfte sein. Die Hälfte der Läufer mit 3 Std hat das hier so „durchgezogen“. Die Grafik zeigt aber auch, dass es Manchem mit einem schlechterem split z.B. 10% trotzdem gelingt die 3:00 zu erreichen. Nur sind das dann eben sehr wenige oder anders ausgedrückt „Ausnahmen“. Bei 4:00 Stunden Zielzeit kann man sich dann schon 5% Zuschlag leisten.
Die Quantillinie wurde mit einer parametrischen Quantilregression bestimmt (vgl. weiter unten) und fällt schon ganz gut mit der TLS Linie zusammen. Das ist kein Zufall, da die TLS Linie der Eigenvektor zum betragsgrößten Eigenwert der Verteilung (Time,Split) ist. Dann nämlich sollte links und rechts davon ungefähr die selbe Masse liegen. Im Unterschied zum Eigenvektor ist die Quantillinie aber nicht an Linearität gebunden.
Age Grading
Die Altersklassen des DLV ermöglichen eine Differenzierung der Laufleistung nach dem Alter. Sie sind zugleich Ansporn für viele Läufer, sich gut im jeweiligen Alterssegment zu positionieren. Beim sogenannten „Age Grading“ versucht man nun einen Vergleich über Altersklassen hinweg aber unter Ausschaltung des Alterseinfluss vor zunehmen. Wie kann man sich das vorstellen?
Dazu ist folgendes Gedankenexperiment instruktiv. Angenommen, wir hätten von einer großen Menge von Läufern die Finishzeiten auf einem Marathon gemessen. In darauf folgenden Monaten oder Jahren messen wir wieder die Finishzeiten auf der selben Strecke und bei genau den gleichen Läufern. Man wird dann trotz gleicher Bedingungen sehr wahrscheinlich abweichende Zeiten messen. Dafür kann es sehr viele Ursachen geben, z.B. Tagesform, Trainingsstand, Krankheit, Ausrüstung, Wetter etc. Letztlich konnte man viele Einflussfaktoren eben über die Zeit t und damit auch über das Alter a nicht konstant halten. Man kann dann vermuten, dass sich im Mittel diese zufälligen Faktoren ausgleichen (vgl. dazu auch zentralen Grenzwertsatz). Das einzige systematisch variierte Element ist somit die Zeit und das davon abhängige Alter a(t) der Läufer. Die Laufleistung eines Läufers i zum Zeitpunkt t wäre dann Finishzeiti,t = αa(i,t) + εi,t. ε sind hier die zufälligen Änderungen – wie die zuvor genannten – von denen wir annehmen, dass sie im Mittel keinen Einfluss haben. αa(i,t) ist dann der Einfluss des Alters auf die Finishzeit. Dieses Modell kann man noch verfeinern, in dem man individuelle Aspekte der Läufer i berücksichtigt also z.B. Finishzeiti,t = αa(i,t) + βi + εi,t wobei die additive Verkettung der Einflussfaktoren sicherlich nicht die einzig sinnvolle ist. Das gleiche gilt für den Fehlerterm ε der sicherlich differenzierter modelliert werden sollte.
Unabhängig davon, wie die genaue Modellierung der Einflussfaktoren und des Fehlers erfolgt, kann man nach Schätzung des Einflusses diesen aus den Messungen entfernen und wir erhalten die altersbereinigten Finishzeiten. In der hier angenommen Situation – es sind die gleichen Läufer unterwegs – sollten dann die bereinigten Werte der verschiedenen Altersklassen aus ein und der selben Verteilung stammen.
Der Effekt des Age Gradings besteht darin, die altersabhängigen Verteilungen der Finishzeiten ineinander zu überführen.
Das sollte auch näherungsweise für Situationen gelten, in denen die Läufer nicht konstant gehalten werden, sondern ebenfalls „zufällig“ antreten. Für die Spitzenläufer und Topzeiten ist diese Annahme sicherlich problematisch, da das Preisgeld eine Einfluss darauf hat, wer zum Marathon erscheint. Für die restlichen 99% der Freizeitläufer, die nie auf dem „Treppchen“ stehen ist dies aber irrelevant.
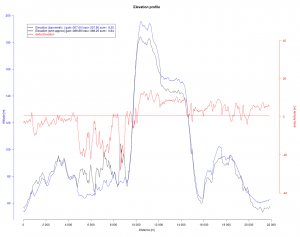
Ein anderer wichtiger Einflussfaktor der in realen Situationen variiert ist die Strecke. Sicherlich kann man die Ergebnisse eines flachen Marathons (Berlin) nicht mit denen einer profilierten Strecke in Zermatt vergleichen. Hier wäre sicherlich ein Flachstreckenäquivalent (vgl. mein Beitrag dazu Höhe Laufen) sinnvoll. Dies könnte man zu einer alterskorrigierten Dauerleistung in Watt (vgl. mein Beitrag Laufleistung) ausbauen und hätte so eine noch größere Datenbasis. Etwas ähnliches gilt für das Geschlecht. Dies ist relativ einfach – da nur 2 Ausprägungen – zu schätzen sind und alle mir bekannten Agegradingmethoden sind geschlechtsspezifisch. Man kann sicherlich die Liste der relevanten Faktoren noch weiter ergänzen. Einerseits reduziert sich damit die Residualstreuung εi,t, andererseits könnte der Alterseinfluss geschmälert oder erhöht werden, je nachdem wie die zusätzlichen Faktoren mit dem Alter korreliert sind.
Wenn man also den Einfluss des Alters – des Jahrgangs/der Kohorte – eliminiert hat und Strecke sowie Geschlecht konstant hält, gibt es keinen Grund mehr zwischen den Altersklassen zu differenzieren und wir können ein Ranking bezüglich der bereinigten Zeiten über alle Altersklassen hinweg vornehmen. Somit wird eine Leistung von Dennis Kimetto 2:02:57 in der MHK (Marathonbestzeit) vergleichbar mit 3:25:43 in der Klasse M80 von Ed Whitlock.
Aus dieser Herleitung resultiert die Anforderungen an die Age Grading Verfahren, die altersabhängigen Verteilungen ineinander zu überführen. Die Kenntnis der Verteilung ist dafür Voraussetzung und mit den Boxplots am Anfang dieses Beitrags haben wir genau das analysiert. Wenn man die Fiinishzeit mit einem Gewicht multipliziert – wie es beim WMA Ansatz gemacht wird – verändert das nicht nur den Erwartungswert sondern auch deren Varianz. Für ab der MHK steigende Gewichte wird so implizit angenommen, dass nach der MHK die Streuung zunimmt. Für den hier vorliegenden Marathon scheint dies nicht gegeben zu sein. Im Gegenteil: die MHK hat die größte Streuung und es spricht einiges dafür, dass dies auch bei anderen Marathons der Fall sein wird, da sich die MHK aus erfahrenen Profis als auch Neulingen zusammensetzt.
Die Altersbereinigung wird im Einzelfall nie exakt gelingen und wir müssen mit Abweichungen vorlieb nehmen. Sind alle Abweichungen gleich „schädlich“? Dies hängt von der Fragestellung ab:
- Möchte man Aussagen zu den altersabhängigen Bestleistungen machen, wird man Fehler am linken Rand der Verteilung (kleine Zeiten) hoch gewichten um sie zu vermeiden. Im Extremfall kann man sogar den Rest der Verteilung (der Messwerte) ignorieren (Gewicht=0).
- Möchte man hingegen eher Aussagen für die Masse – das sind wir Freizeitläufer – machen, wird man sich eher am Mittel der Verteilung z.B. dem Median orientieren.
- Schließlich kann man versuchen sowohl für die Verteilungsränder als auch die Masse differenzierte Aussagen zu machen.
Verteilung der Laufzeiten
Die Laufzeitverteilung hat beim Agegrading eine zentrale Bedeutung, und mit dem Eingangs dargestellten Boxplot haben wir schon eine Vorstellung zur Verteilung gewonnen. Man kann das noch detaillierter darstellen, da der grouping Faktor des Boxplots – die Altersklassen – kardinal skaliert ist und man annehmen kann, dass über die Altersklassen hinweg ein kontinuierlicher Prozess wirkt, nämlich das „Altern“.
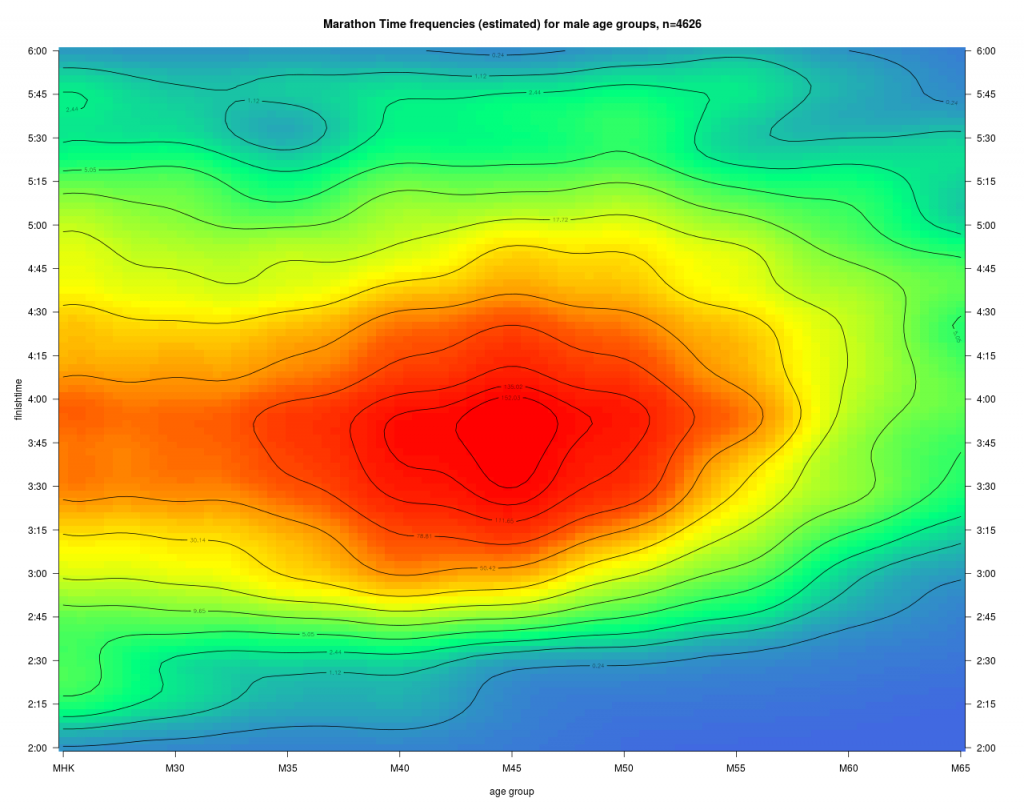
Diese Dichte zu den Laufzeiten zeigt deutlich den Häufungspunkt bei M45 und 3:45. Daneben erkennt man unten die Kontourlinie für die Bestleistungen (1%) dieses Marathons. Mit zunehmendem Alter steigt diese erwartungsgemäß an. Für den Läufer ist nun die daraus abgeleitet kumulierte Verteilung interessant.
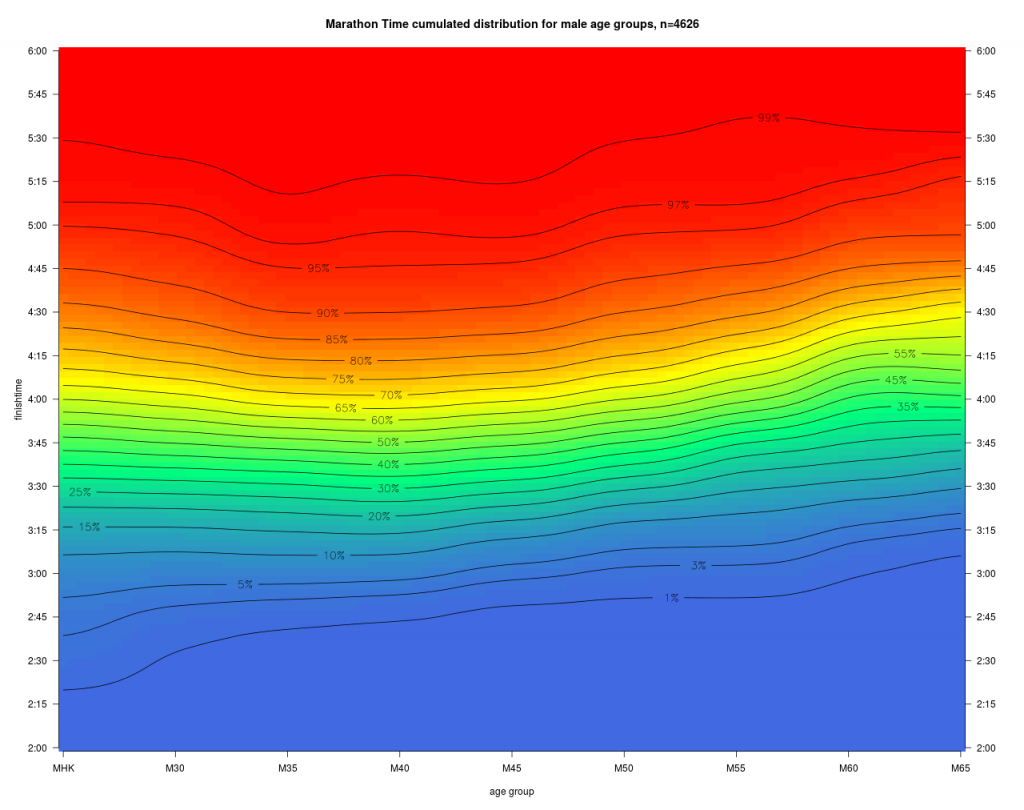
Farbe und Höhenlinien geben nun die Wahrscheinlichkeit an, dass ein Läufer der AK a das Ziel vor der Zeit t erreicht.
Beispiel: Mit einer Wahrscheinlichkeit von 95% erreicht ein Läufer der MHK das Ziel vor 5:00 Stunden.
Daneben erkennt man unten die 1% Linie, also nahe den Altersbestzeiten dieses Marathons. Diese Linie steigt über den gesamten Altersbereich von ca, 2:17 auf ca. 2:45 Zielzeit für die M65 an. Man sieht auch, dass im mittleren Leistungsbereich von z.B. 50% die Höhenlinien sich deutlich anders mit dem Alter entwickeln als die Bestleistungen. Jede dieser Linien kann man als Menge leistungsäquivalenter Zeiten auffassen, und man hat damit schon einen ersten Ansatz für ein „Age Grading“. Diese fällt für Topläufer offensichtlich anders aus, als für die Masse der Freizeitläufer, was auch den Eingangs dargestellten Überlegungen zur maximalen Altersleistung entspricht. Man sieht hier schon gut, dass die Übertragung der Topläufer Altersdegression auf die Masse der Freizeitläufer zu einer Fehleinschätzung führt. Würde man die Topläufer Degression auf eine Laufleistung von 90% übertragen würden die Alterszuschläge deutlich überschätzt.
WMA and USATF
Das Vorgehen und die Daten sind usatf entnommen und der Zusammenhang wird am Beispiel der Marathon Distanz dargestellt.
Die Berechnungen fußen auf einem geschlechtsspezifischem OpenClassStandard OC(gender) und Age Factors AF(gender,age)<1. Aus diesen wird der Age Standard mit AS(gender,age)=OC(gender) / AF(gender,age) berechnet. Die relative Performance P(i) einer Leistung T(i) ergibt sich dann aus P(i)= AS(gender,age)/T(i) die i.d.R ≤ 1 ist.
Rechenbeispiel
gender=male, age=40, => AS(male,40)= 126,426735 min
T(i)= 3:30 = 210 min
P(i)= 126.426735/210= 60.20 %
Die so berechneten P(i) sind über verschiedene Distanzen, Geschlechter und Alter vergleichbar. Für das Age grading ist nun der Zusammenhang zu anderen Alterswerten interessant. Wir nehmen an, ein Läufer habe gleichwertige Ergebnisse zum Zeitpunkt a und a+t erzielt, also
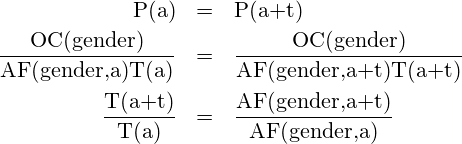
Dann müssen die beiden Zeiten T(a+t) und T(a) im selben Verhältnis stehen wie die Altersfaktoren, unabhängig vom OpenClassStandard OC. Wie kann das sein?
Dies erschließt sich einem durch die Ableitung der Altersfaktoren, vgl. AgeGrade. Dazu wird auf einer Datenbasis eine untere Grenze für den AgeStandard AS=AS(a) geschätzt. AS(a) ist ein über 7 Altersabschnitte definiertes Polynom, das an den Nahtstellen stetig und differenzierbar ist.
Die AS(a) sind also kleiner gleich den altersspezifischen Bestzeiten. Der Altersfaktor ist dann mit min(As(a))/As(a) <= 1 gegeben.
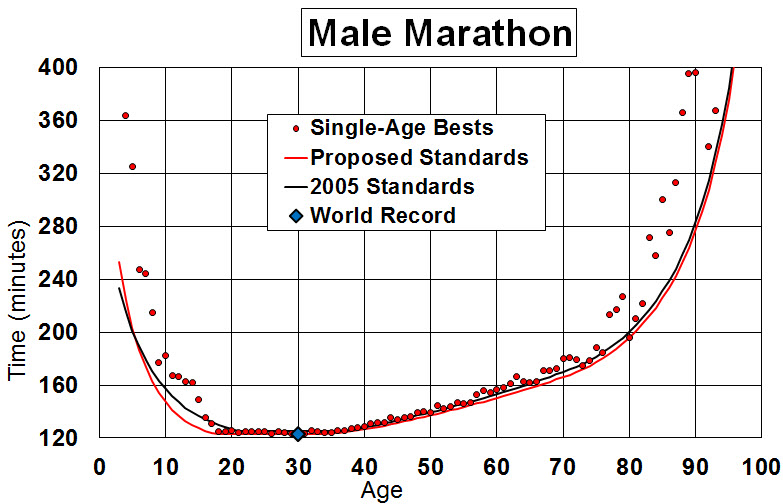
Quelle: Alan Jones
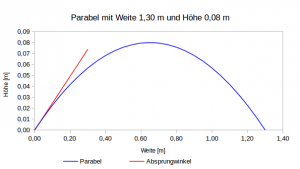
Die rote Linie in der vorausgegangenen Grafik stellt dann die altersäquivalenten Leistungen dar. Die Weltbestzeit liegt genau auf dieser Linie. Der Punkt (age ≈ 92, time ≈ 340) gehört zur unteren konvexen Hülle der hier dargestellten Menge (rote Punkte), liegt aber oberhalb dieser Linie und wäre damit schlechter zu bewerten. Warum? Dies liegt hier an der angenommenen Polynomform der Beziehung. Man kann dies sicherlich hinterfragen, da eine flexiblere Funktionsform (z.B. könnten mit splines ebenfalls monoton steigende Zusammenhänge jenseits der 30 nachgebildet werden) diesen Punkt tangieren würde. Im Fazit hat man auch hier mit einer gewissen Unschärfe zu rechnen.
In DeriveAgeGrades wird ein rekursives L2-Norm fitting Verfahren beschrieben (…You start by fitting a curve that runs through the middle of the data…) das sukzessive Punkte aus der Schätzung entfernt die über der Regressionsfunktion liegen. Der Abbruch des Verfahrens ist jedoch in der Quelle nicht beschrieben, da jede weitere L2 Regression wieder positive als auch negative Residuen produziert.
Aus Sicht des Autors könnte man dies eleganter mit einer 100% parametrischen Quantil Regression erreichen, was im folgenden Abschnitt auch dargestellt wird. Daneben gilt es den Effekt von Fehlern – nicht nur in der Messung sondern auch in der Datenverarbeitung – zu bedenken. Da die Ergebnisse des WMA -Ansatz nur an wenigen Punkten hängen, können hier Fehler nicht mehr durch die große Anzahl von tausenden von Beobachtungen ausgeglichen werden. Man muss hier also schon sehr sicher sein, dass keine großen Fehler in den Daten enthalten sind und diese vertrauenswürdig sind (vgl. Alan Jones).
Neben diesen methodischen Fragen, soll hier festgehalten werden, dass die Altersfaktoren letztlich normierte Extrema darstellen.
Age Grading für Freizeitläufer
Der WMA-Ansatz orientiert sich an den Weltbestleistungen in jeder Altersklasse. Formal entspricht das einem 100% Quantil der altersabhängigen Geschwindigkeitsverteilung.
Haben 2 Leistungen mit unterschiedlichem Alter den gleichen relativen Abstand zu den zugeordneten Bestleistungen sind sie demnach äquivalent. Dies mag für Leistungen nahe der Bestleistungen auch zu realistischen Einschätzungen führen. Wir Freizeitläufer sind aber in der Regel meilenweit von solchen Bestleistungen entfernt. Wenn man von dem maximal Erreichbarem weit entfernt ist, kann man vermuten, das die altersbedingte Degression schwächer ausfällt, da die physiologischen Grenzen nicht ganz so restriktiv wirken. Der Freizeitläufer hat in diesem Bereich noch immer Steuerungsmöglichkeiten wie z.B. Training, Technik und Ernährung mit denen er altersunabhängig seine Laufleistung verbessern kann. Die Weltbestläufer haben demgegenüber kaum noch Steuerungsmöglichkeiten, da alle Instrumente weitgehend erschöpft sind.
Für uns Freizeitläufer ist der Bezug zum 100% Quantil der WMA nicht besonders instruktiv und kann auch zu Fehleinschätzungen führen, wie später gezeigt wird. Die meisten von uns werden nie diese Altersbestleistungen erreichen und somit auch nicht zum 1‰ Quantil der Altersklasse gehören (… dazu sind mindestens 1000 Läufer in der AK erforderlich). Deshalb werden hier relevante Quantile berechnen. Dazu setzen wir eine parametrische Quantile Regression an
![\begin{eqnarray*} P_{i,j}(\tau_j,x_i,\sigma_i) & =& \min\limits_{\beta,\epsilon_{+}\ge 0,\epsilon_{-}\ge 0} w^T(\epsilon_{+} + \epsilon_{-})\\ \mbox{\small Finishtime} & = & \left[ 1, \mbox{\small age} \right] \beta + \left[ \epsilon_{+}, \epsilon_{-} \right] \left[\begin{array}{l} \tau_j\\ \tau_j -1 \end{array}\right] \\ w & = & \mbox{N}(x_i,\sigma_i)\\ \end{eqnarray*}](https://lt-pappelallee.de/wp-content/ql-cache/quicklatex.com-a3edeb99997ec7aa7456efa2a44eaaf3_l3.png "Rendered by QuickLaTeX.com")
und lösen diese Probleme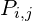 
für das Kreuzprodukt 
. 
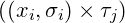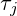ist hier das betrachte Quantil und mit 
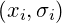wird der betrachtete bzw. hoch gewichtete Altersbereich (
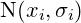=Normalverteilung) festgelegt. Wenn man hier 
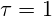setzt, ist die Finishtime stets kleinergleich der Schätzung d.h. man hat so das Infimum zu den Bestzeiten geschätzt. Das Infimum muss aber nicht notwendigerweise mit der unteren konvexen Hülle zusammen fallen, sondern wird hier einen eher „zackigen“ Verlauf haben. Man kann nun vermuten, dass mit zunehmenden Datenerhebungen diese „Zacken“ verschwinden und deshalb einer unzureichenden Stichprobe geschuldet sind. Diese Glättung kann man in der Quantil-Regression mit der Bandbreite σ der Gewichte w erreichen. Man muss hier aber bedenken, dass man damit einzelne Topleistungen evtl. leicht zu „2. klassig“ degradiert. Der hier skizzierte Quantil-Regressions Ansatz wäre sicherlich förderlich für das WMA-Modell zu den Bestleistungen.
Der parametrische Ansatz hat gegenüber dem WMA Ansatz den Vorteil, dass wir keine Funktionsform vorgeben müssen und somit davon unabhängige Ergebnisse erzielen, die im Folgenden dargestellt sind.
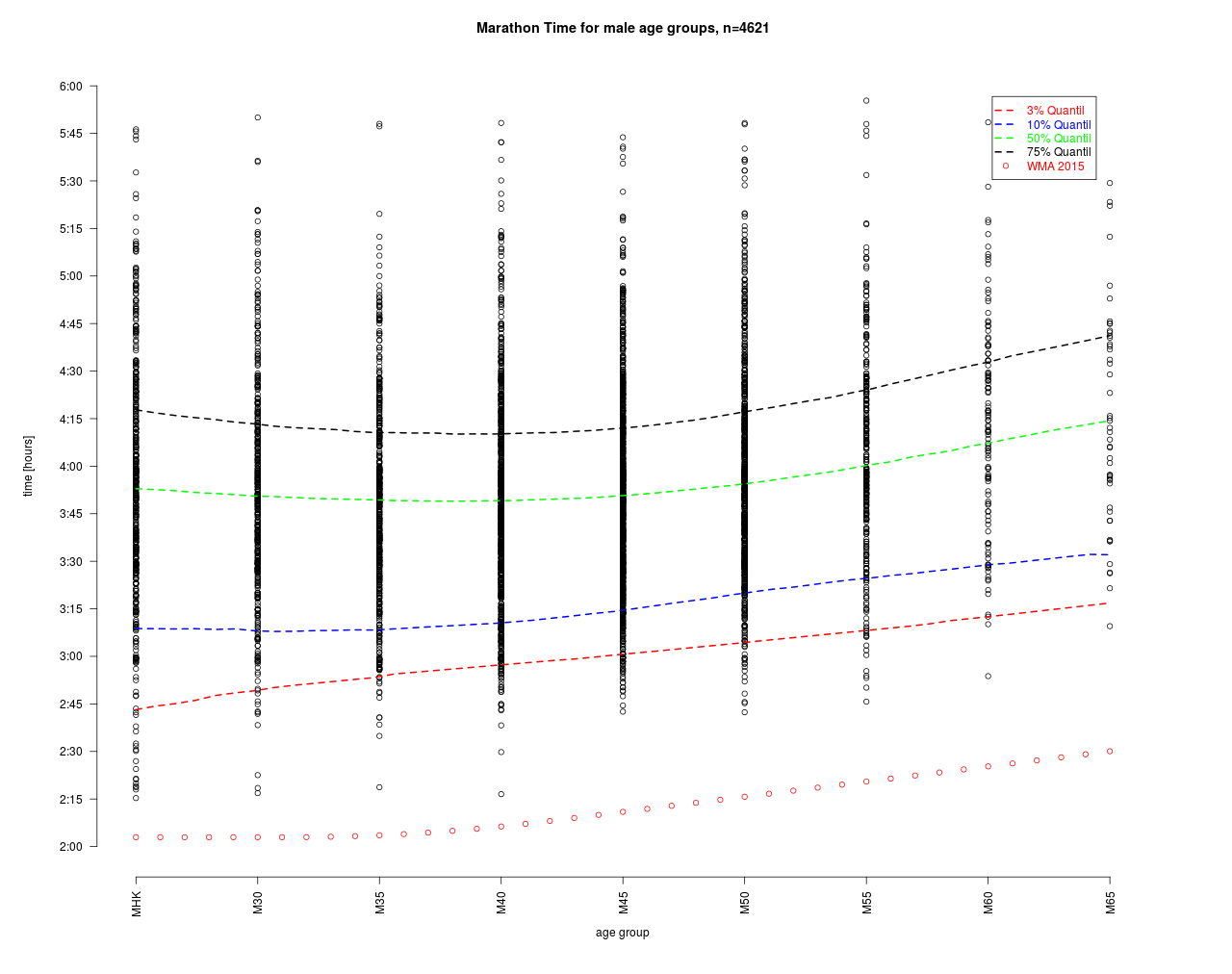
Die Schätzung zu den Quantilen zeigen einen deutlich unterschiedlichen Verlauf. Bei den Topläufern liegt eine starke Altersdegression vor während das Mittelfeld eher den bereits bekannten „Bauch“ bei M40 hat. Die WMA-Zahlen liegen erwartungsgemäß deutlich unter den Bestwerten dieses Marathon. Die Umrechnung der Quantile auf die MHK ist im Folgenden grafisch dargestellt.
Auc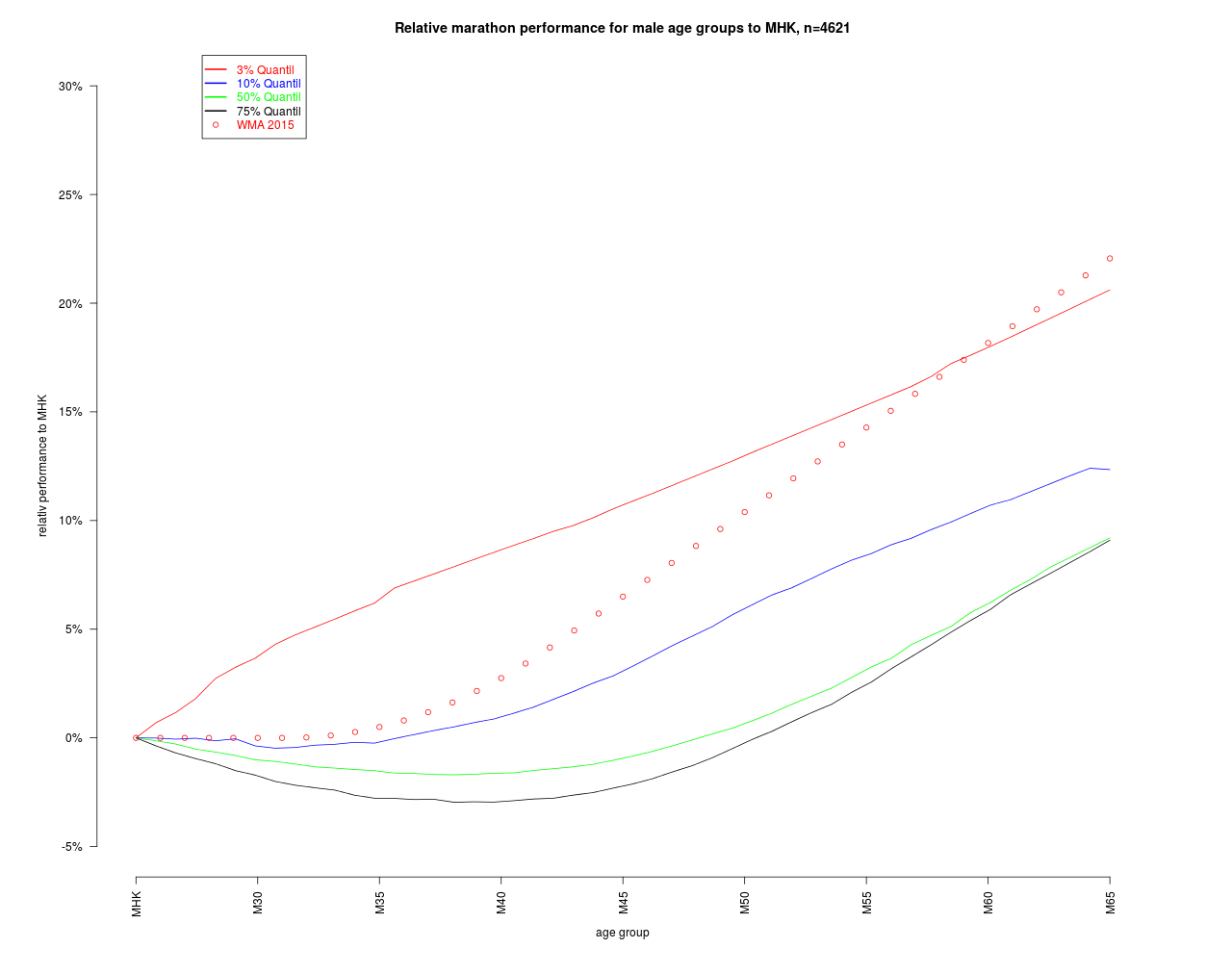
Zunächst fällt auf, dass für die mittleren Leistungsgruppen bis M50 kein Alterszuschlag nötig ist.Wenn man stets mittleres Tempo läuft, hat man erst in späten Jahren mit Zuschlägen zu rechnen. Das WMA Modell würde hier zu einer Überschätzung des Alterseffekts führen. Anders ausgedrückt: Mit dem WMA Modell kann man sich „gesund“ rechnen bzw. werden Älteren MHK-Zeiten zugewiesen, die wahrscheinlich nie erreichbar waren. Das WMA Modell würde dies für alle Leistungsklassen gleichermaßen machen. Das hier vorgestellte Modell ist differenzierter. Läuft man im fortgeschrittenen Alter einen Marathon in den besseren Rängen, fallen auch die Abschläge auf MHK größer aus. Läuft man eher mittleres Tempo, kann das auch zu keinen Abschlägen und in machen AK 30-35 auch zu Zuschlägen führen.
Wie kann man nun diese Ergebnisse auf Stabilität prüfen oder anders gefragt: Wie groß sind die Vertrauensbereiche? Dies kann hier relativ einfach abgeschätzt werden, da eine vollständige Zeitreihe über mehr als 10 Jahre vorliegt. Wenn man dann einen Datensatz zu einem weiteren Marathon Jahr hinzunimmt (vgl. Cross-validation), sollten sich die Ergebnisse nicht stark verändern. Bei Aufbau dieser Studie wurden sukzessive Datensätze hinzugefügt und es zeigte sich nach einer gewissen Zeit ein stabiles Bild. Das Modell ist also sicherlich nicht overfitted.
Übertragbarkeit
Natürlich hat die Datenbasis einen entscheidenden Einfluss auf die Ergebnisse. Ansonsten wäre die Analyse und das Modell ja invariant gegenüber der gemessenen Realität und würde den Namen empirisch nicht verdienen. Es stellt sich deshalb die Frage wie repräsentativ die Daten sind. Mögliche Einflussgrößen sind
- Art der Strecke wie Höhenmeter, Untergrund, absolute Höhe haben Einfluss auf die Verteilung der Ergebnisse
- Preis- und Startgeld ziehen Topläufer an
- Eintrittsgeld kann abschreckend wirken
- Bekanntheit der Veranstaltung sorgt wahrscheinlich eher für einen höheren Anteil Topläufer
- Zeitliche Lage im Kalender insbesondere Konkurrenz zu anderen Veranstaltungen können auch die Verteilung prägen
- Wetter bei der Veranstaltung: Dauerregen, Eis ist nur etwas für die hart gesottenen, verschlechtert aber das Ergebnis
- Service und Goodies ziehen die Massen an
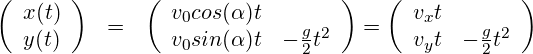
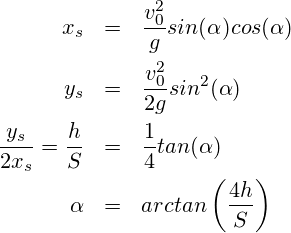
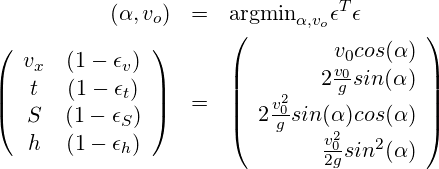
![\[ \frac{60}{\mbox{Schrittfrequenz}} = \mbox{Bodenkontaktzeit} \]](https://lt-pappelallee.de/wp-content/ql-cache/quicklatex.com-20bd818bc4ea02b62080c7b8b8bbf479_l3.png "Rendered by QuickLaTeX.com")
wobei SF die Schrittfrequenz ist.
: Geschwindigkeit beim Absprung in Richtung α
gleichförmige und ungebremste Bewegung mit der horizontlen Komponente von 
,
durch Schwerkraft 
gebremste Bewegung 
.
der Wurfparabel
berechnet und dann über eine weiter Gleichung 
bestimmt hat man sämtliche Parameter zur Parabel festgelegt. Wendet man dies nun auf mit einer Laufuhr gemessene Werte an, stellt man i.d.R. fest, dass die unberücksichtigt geblieben Gleichungen nicht erfüllt werden d.h. man hat Fehler in den Gleichungen zu 
. Dies kann einerseits daran liegen, dass das Modell zu einfach und damit falsch ist, andererseits könnten Messfehler das Bild trüben. Aus den Beitrag zur Höhe wissen wir, dass die per gps-Uhr gemessene Geschwindigkeit fast nie mit dem Quotient aus Länge und Zeit übereinstimmt, weil 
z.B. über einen Kalman Filter ermittelt wird. Deshalb wird im Folgenden versucht die Fehler auszugleichen.
im Rahmen eines nichlinearen Modells zu bestimmen.
: die per gps gemessene Geschwindigkeit [m/s]
: die Zeit pro Schritt aus 
Kadenz abgeleitet [s]
: die Schrittweite [m] aus 
abgeleitet
: der vertikale Hub [m] nach Garmin HRM Messung![\[\begin{array}{lrrr} & \mbox{observed values} & \mbox{commercial Solver} & \mbox{CG Verfahren} \\ \hline $v & 3.4150 & 3.7736 & 3.4675 \\ t & 0.3704 & 0.2903 & 0.2735 \\ x & 1.2648 & 1.0954 & 0.9482 \\ y & 0.0917 & 0.1033 & 0.0917 \\ \hline \hat{\alpha} & & 20.67145 & 21.14802 \\ \hat{v}_0 & & 4.0332 & 3.71786 \\ \hline e_v & & 0.3586 & 0.0525 \\ e_t & & -0.0801 & -0.0969 \\ e_x & & -0.1695 & -0.3166 \\ e_y & & 0.0116 & 0.0000 \\ \hline e_v \% & & 10.50\% & 1.54\% \\ e_t \% & & 21.63\% & 26.17\% \\ e_x \% & & 13.40\% & 25.03\% \\ e_y \% & & 12.67\% & 0.00\% \\ \hline \hline \mbox{objective} & & 14.5491\% & 13.1833\% \\ \end{array}\]](https://lt-pappelallee.de/wp-content/ql-cache/quicklatex.com-c546e98c1eaf897ae7d1883337a6612d_l3.png "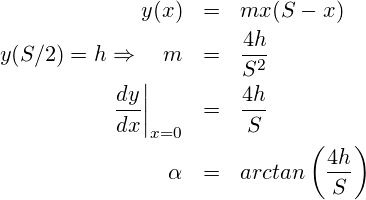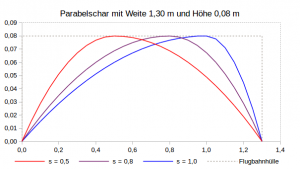Rendered by QuickLaTeX.com")
wird aber der Absprungwinkel mit ca 21. Grad geschätzt. Unbefriedigend sind hingegen die Anpassungen an t und x und die damit assoziierte Kadenz und Schrittweite.
und desto niedriger die Masse des bewegten Körpers ist.
mit Form 
ergeben sich die Parameter
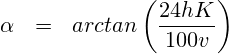
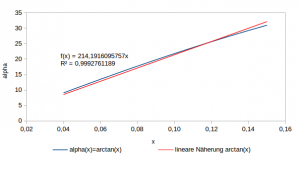
![\[\begin{array}{lccc} & a & b & c \\ \hline \mbox{Parabel 1} & -\frac{h}{s^2} & \frac{2h}{s} & 0\\ \mbox{Parabel 2} & -\frac{h}{(S-s)^2} & \frac{2hs}{(S-s)^2} & \ldots \end{array} \]](https://lt-pappelallee.de/wp-content/ql-cache/quicklatex.com-73fc7393a5e7fdf48e3a555d1836ce83_l3.png "Rendered by QuickLaTeX.com")
und liefert für 
natürlich den Wert der Wurfparabel. Für realistische Flugbahnen dürfen aber eher Werte 
relevant sein die zu einem kleineren Absprungwinkel führen. Unterstellt man bei einem Lauf ein konstantes Verhältnis von 
so sind die berechneten Steigungen des zusammengesetzten Modells und des Wurfparabelmodells proportional. Bis auf einen – hier leider unbekannten – positiven Skalierungsfakor ändert sich nichts, und wir können dennoch Richtungsaussagen machen.Unter Verwendung der Definitionsgleichung für die Schrittlänge 
und dem Absprungwinkel der Wurfparabel erhält man
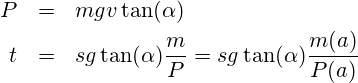
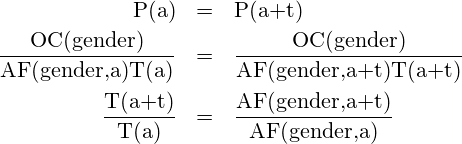
![\begin{eqnarray*} \alpha & \approx & c \frac{h K}{v} \\ v \alpha & \approx & c \underbrace{h \,\, K}_{\mbox{Hubleistung [m/min]}} \end{eqnarray*}](https://lt-pappelallee.de/wp-content/ql-cache/quicklatex.com-6f5e8b0c24a4c1346ef927dbee220ca4_l3.png "Rendered by QuickLaTeX.com")
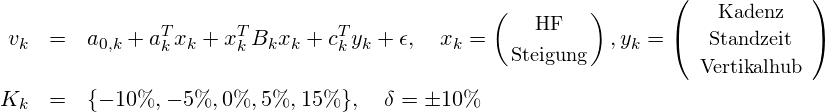
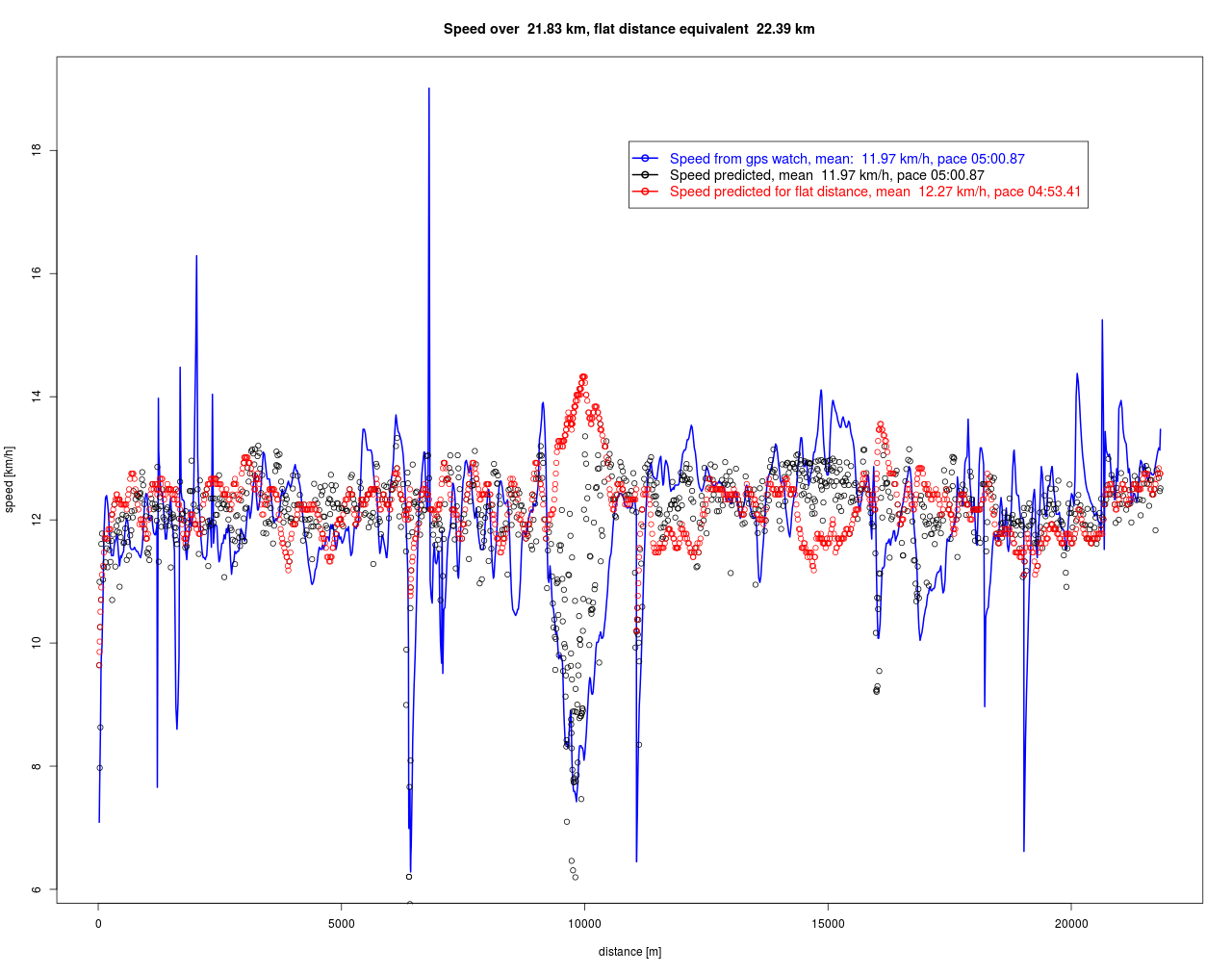
![\[ \mbox{HM} = \sum_t \max{(H_t-H_{t-1},0}) = \sum_t \max{(\Delta H_t,0})\]](https://lt-pappelallee.de/wp-content/ql-cache/quicklatex.com-5605a1b2723746000112163622eadb41_l3.png "Rendered by QuickLaTeX.com")
für ein Segment i erfolgen. Da die Zeit gut – ohne Fehler – gemessen werden kann, hängt nun der Fehler von der Geschwindigkeitsungenauigkeit ab. Da die Geschwindigkeit i.d.R bei einer GPS Laufuhr mit einem Glättungsverfahren z.B. 
für die Residuen nachgebildet.
der benachbarten Polynome ausgewertet.
![\[ c = \frac{\bar{v}}{\bar{\hat{v}}}, \quad \bar{v}= \frac{ \sum_i \mbox{\small distance}_i}{\sum_i t_i}, \quad \bar{\hat{v}} = 1/N \sum_i^N v(\mbox{\small HF}_i, \mbox{\small Steigung}_i) \]](https://lt-pappelallee.de/wp-content/ql-cache/quicklatex.com-1095f149f52780055e1fd9347bc85da2_l3.png "Rendered by QuickLaTeX.com")
ist dann die geschätzte Geschwindigkeit zu gegebener Herzfrequenz (i) und Steigung (i) die im Mittel mit den Daten der Laufuhr übereinstimmt. Für das Flachstreckenäquivalent müssen jetzt nur noch die Werte 
berechnet werden. Diese sind in der folgenden Grafik dargestellt.
![\[ \begin{array}{lcl} % P(t)_{\mbox{\small Hubleistung}} & = & m_{\mbox{\small Läufer}} g H(t) \,\, K(t) \\ P(t)_{\mbox{\small Beinbeschleunigung}} & = & c K(t) \\ P(t)_{\mbox{\small Luftwiderstand}} & = & \frac{1}{2} r_{\mbox{\small Luft}} A_{\mbox{\small Läufer}} c_{w \,\mbox{\small Läufer}} v(t)_{\mbox{\small Läufer}}^3\\ P(t)_{\mbox{\small netto}} & = & P(t)_{\mbox{\small Hubleistung}} + P(t)_{\mbox{\small Beinbeschleunigung}} + P(t)_{\mbox{\small Luftwiderstand}}\\ P(t)_{\mbox{\small brutto}} & = & \frac{1}{\eta} P(t)_{\mbox{\small netto}} + P(t)_{\mbox{\small Grundumsatz}}\\ W_{\mbox{\small Lauf}} & = & \sum_i t_i P(t_i)_{\mbox{\small brutto}} \\ \hline \multicolumn{3}{l}{ \mbox{\small mit: } t= \mbox{\small Zeit}, H(t)=\mbox{\small vertikal Hub}, K(t)=\mbox{\small Kadenz}, v(t) =\mbox{\small Geschwindigkeit}, W_{\ldots} = \mbox{\small Arbeit}, P_{\ldots} = \mbox{\small Leistung}}\\ \multicolumn{3}{l}{ \mbox{\small und Parametern: } m=70,\quad g =9.81,\quad c=10,\quad r A c_w/2= 0.2889378414\quad \eta=0.21 } \end{array} % \]](https://lt-pappelallee.de/wp-content/ql-cache/quicklatex.com-6eb72236cc600153f0b307615fc3f783_l3.png "Rendered by QuickLaTeX.com")
so ergibt sich, da 
. Bei konstanter Hubleistung, Hub und Schrittweite führt eine um 1% gesteigerte Masse zu einer Geschwindigkeitssenkung von ebenfalls 1%. Leichte Läufer sind hier also im Vorteil, und so etwas ähnliches besingen auch „Silbermond“ mit
![\[ P_{\mbox{\small Hubleistung}}= m\, g\, v\, tan(\phi) \]](https://lt-pappelallee.de/wp-content/ql-cache/quicklatex.com-334a5d8b46e5f51b1a493cdec1bed4bd_l3.png "Rendered by QuickLaTeX.com")
) sind diese Werte besonders unangenehm. Deutlich erkennbar sind einige schnellere Runden am Anfang sowie gemütliches Laufen in der zweiten Hälfte. Die dicken blauen Linien sind das 5%, 50%, 95% Quantil der gemessenen Geschwindigkeiten. 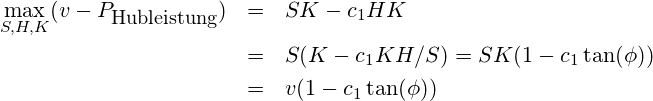Mit roten Punkten sind die abgeleiteten Nettoleistungen dargestellt und es lässt sich schon hier ein enger Zusammenhang vermuten.![\[ W_{\mbox{\small Bein}} = \frac{1}{2} m_{\mbox{\small Bein}} v_{\mbox{\small Bein}}^2 \]](https://lt-pappelallee.de/wp-content/ql-cache/quicklatex.com-dd8ce58c0a6d3aafad6332ff3a9cfd5b_l3.png "Rendered by QuickLaTeX.com")
![\begin{tabular}{lrrrr} Masse & 70 & 70 & 70 & 70 \\ Beinmasse & 8,75 & 8,75 & 8,75 & 8,75 \\ \hline Pace [min/km] & 3:20 & 4:10 & 5:00 & 6:00\\ Speed [km/h] & 18 & 14,4 & 12 & 10 \\ v [m/s] & 5,00 & 4 & 3,33 & 2,78\\ \hline WB [J] & 109,38 & 70 & 48,61 & 33,76\\ Kadenz [1/min] & 150 & 150 & 150 & 150\\ Zeit pro Schritt [s] & 0,4 & 0,4 & 0,4 & 0,4\\ \hline P(B) [W] & 273,44 & 175,00 & 121,53 & 84,39 \end{tabular}](https://lt-pappelallee.de/wp-content/ql-cache/quicklatex.com-3621c08ef506bd6fccec8f6d312c1665_l3.png "Rendered by QuickLaTeX.com")
verstärkt werden. Deshalb wird dieser Ansatz zunächst nicht weiter verfolgt.
