Höhe Laufen

Berge hoch zu laufen ist eine besondere Anforderung an jeden Läufer. Wir haben hier in der rheinischen Tiefebene natürlich keine großen Höhenunterschiede aber im Bergischen Land gibt es schon einige Anstiege mit 20%, unter anderem an der Wupper zwischen Solingen und Leichlingen der asphaltierte Anstieg „Fähr-Rödel“.
Nach einem Lauf mit Laufuhr fragt man sich dann unweigerlich, wie viele Höhenmeter (HM) man geschafft hat. Das ist die Summe aller positiven Höhenänderungen
![]()
und somit mit der Höhenmessung Ht zum Zeitpunkt t verbunden.
Höhenmessung
An der Definitionsgleichung zu den Höhenmetern erkennt man, dass ein Versatz der Höhe um einen konstanten Betrag keinen Einfluss auf die Höhenmeter hat. Anders sieht es aus, wenn die Höhenmessung um unterschiedliche Beträge versetzt sind d.h. es liegen Messfehler vor . Hier wirkt sich das max(…) in der Definition zu den HM besonders negativ aus, da sich Über- und Unterschätzungen der wahren Höhendifferenz kaum noch kompensieren können. Deshalb kommt der genauen Höhenmessung eine zentrale Rolle zu. Zur Ermittlung der Höhenmeter gibt es derzeit im wesentlichen 3 Methoden:
- Die Laufuhr verfügt über ein Barometer und ermittelt über Luftdruckunterschiede (Höhenmessung) die Höhe mit den in der Quelle genanntem Probleme. Häufig kommt es vor, dass man zu Laufbeginn vergessen hat das Gerät zu kalibrieren, so dass die Höhen um einen Betrag verschoben sind. Man kann dann, sofern man eine Höhe kennt, die abgeleitete Höhendifferenz von allen anderen Höhen abziehen. Ein anderes Problem sind Änderungen im Luftdruck (schönes Wetter -> Hochdruck) die die Messung beeinträchtigen kann.
- Die Laufuhr hat kein Barometer und ermittelt die Höhe über das GPS-Signal. Diese Methode ist relativ ungeeignet für die Berechnung des Aufstiegs, da sich hier die GPS-Fehler erheblich akkumulieren und wird in der Praxis kaum genutzt.
- Die Höhenmeter werden nachträglich bestimmt, in dem man aus einer topografischen Datensammlung (z.B. SRTM) mit Höhenangaben zu gegebenen Längen und Breitengrad der Laufuhraufzeichnung die Höhe – durch Interpolation zwischen den Grid-Punkten – bestimmt und darüber die Summe der positiven Anstiege bildet. Ein Problem sind hier Unterführungen und Tunnel, das andere wesentliche Problem sind Ungenauigkeiten in der geographischen Position.
Die Ergebnisse zu Methoden 1 und 3 zum Lauf „Fähr-Rödel“ sind in folgenden Grafik gegenübergestellt.
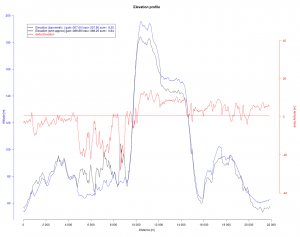
Die barometrische Höhenmessung weist hier den höchsten Punkt aus, aber in Summe nur 307.88 HM. Die SRTM Interpolationsmethode kommt hingegen auf 388.88 HM obwohl hier kein einziger Tunnel durchlaufen wurde und die gps-Aufzeichnung unter günstigen Bedingungen (freier Himmel, Winter d.h. Laubbäume blattfrei, vgl. GPS Genauigkeit) erfolgte. Damit liegt die SRTM Methode 25% über der barometrischen Methode. Schaut man sich die Stellen an, an denen diese Höhenmeter „geschöpft“ werden, so stechen km 5-10 heraus. Das ist an den Wuppersteilhängen gelegen, und somit besonders empfindlich für aus Geopositionen abgeleitete Höhen. Es ist zu vermuten, dass durch die SRTM Methode nicht nur hier sondern generell bei Schluchten und Tälern enorme Fehler entstehen.
Betrachtet man den Graph der barometrischen Höhenmessung und die Karte zum Lauf, fällt auf, das Anfangs- und Endpunkt – obwohl fast gleiche geographische Position – nicht in der Höhe übereinstimmen und somit in Summe ein Fehler von 9.2 m resultiert. Das kann z.B. auf Luftdruckänderungen während des Laufs beruhen (z.B. Aufzug eines Hochdruckgebiets). Die SRTM Methode hat dem gegenüber nur einen Fehler von 0.64 m, ist hier also besser. Ein ähnliches Abwägungsproblem gibt es in der Statistik und wird mit Bias variance tradeoff bezeichnet. Auch hier nimmt man gerne eine kleine Verzerrung zugunsten einer niedrigeren Varianz (in der Höhe) in kauf.
Die Höhenmeter werden also durch die SRTM-Methode nur sehr ungenau ermittelt und sind auch für Vergleiche unterschiedlicher Strecken kaum geeignet. Das machen Läufer aber sehr gerne, sei es in der Vorbereitung eines Wettkampfs oder in der Bestimmung der Leistungsfähigkeit. Hier kommt noch ein weiteres Problem dazu: Wie vergleiche ich Strecken mit unterschiedlichem Höhenprofil?
Längenmessung
Die Längenmessung sollte eigentlich selbstverständlich sein, stößt aber in der Praxis bei GPS-Laufuhren auf Probleme.
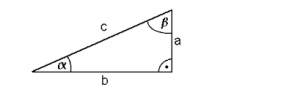
Wenn man einen Berg mit Steigungswinkel α hinauf läuft sollte die Länge der Strecke „c“ (Hypothenuse) in der vorausgegangenen Abbildung als Weglänge angesetzt werden. Rechenbeispiel:
Man läuft 100 m einen Berg mit 10% Steigung hoch. Dann hat man 9.95 m an Höhe gewonnen.
Häufig wird aber für die Weglänge die Strecke b gewählt die sich ausschließlich über die Längen- und Breitengrade der GPS-Punkte berechnen lässt. Dies ist besonders dann ratsam, wenn die Höhendifferenz (Strecke „a“) nur sehr unsicher bestimmt werden kann, z.B. über das GPS Signal und nicht barometrisch. Wie die Hersteller (Garmin, Polar, TomTom, etc.) das derzeit machen ist dem Autor im Detail nicht bekannt und eventuell auch abhängig von der Art der Höhenmessung des Geräts.
Die Längenmessung könnte auch über Geschwindigkeit v und Zeit t mit ![]() für ein Segment i erfolgen. Da die Zeit gut – ohne Fehler – gemessen werden kann, hängt nun der Fehler von der Geschwindigkeitsungenauigkeit ab. Da die Geschwindigkeit i.d.R bei einer GPS Laufuhr mit einem Glättungsverfahren z.B. Kalman Filter berechnet wird – in dem die Systemvergangenheit enthalten ist – kommt man so regelmäßig zu anderen Längen gegenüber der topografischen Bestimmung. Hier stellt sich die Frage, wie ein Laufuhr die durchschnittliche Geschwindigkeit in Echtzeit berechnet. Dies ist für Läufer wichtig, da man sich gerne eine Pace für den Wettkampf vorgibt (virtual runner), und davon ausgeht, dass man sein Ziel erreicht hat, wenn man vor dem virtual runner die Ziellinie überschreitet.
für ein Segment i erfolgen. Da die Zeit gut – ohne Fehler – gemessen werden kann, hängt nun der Fehler von der Geschwindigkeitsungenauigkeit ab. Da die Geschwindigkeit i.d.R bei einer GPS Laufuhr mit einem Glättungsverfahren z.B. Kalman Filter berechnet wird – in dem die Systemvergangenheit enthalten ist – kommt man so regelmäßig zu anderen Längen gegenüber der topografischen Bestimmung. Hier stellt sich die Frage, wie ein Laufuhr die durchschnittliche Geschwindigkeit in Echtzeit berechnet. Dies ist für Läufer wichtig, da man sich gerne eine Pace für den Wettkampf vorgibt (virtual runner), und davon ausgeht, dass man sein Ziel erreicht hat, wenn man vor dem virtual runner die Ziellinie überschreitet.
Damit gibt es also in der Steigungsmessung = Höhe/Länge erhebliche Fehlerquellen und die Werte sind wahrscheinlich nur approximativ verwendbar. Man kann hier auch nicht einfach über mehrere Abschnitte den Mittelwert bilden (der weniger streut), da sich dann in den aggregierten Abschnitten die Höhenmeter evtl. gegenseitig neutralisieren, wenn auf Steigungen Gefälle folgt. Man kann deshalb vermuten, dass mit steigender Häufigkeit/Dichte der Höhenmessung die ausgewiesene Summe der zurückgelegten Höhenmeter steigt.
Flachstrecken-Äquivalent
Das Flachstrecken-Äquivalent (FSÄ) ist sozusagen der Nullpunkt für den Vergleich von Läufen auf unterschiedlichem Höhenprofilen. Man rechnet die zu vergleichenden Läufe auf das FSÄ um und kann darüber die Läufe vergleichen (ordinal Eigenschaft). Das FSÄ gibt zu einem Lauf eine Lauflänge in der Ebene an, die von der Belastung her gleichwertig ist. Im Idealfall gilt dann, dass die Laufzeit für x km im profilierten Gelände gleich der Laufzeit von FSÄ(x) km in der Ebene ist (kardinal Eigenschaft).
Hierzu gibt es einige Standardformeln, vgl. z.B. Naismith’s rule, die aber nicht ohne Kritik geblieben sind.
Kernpunkt des FSÄ ist die Belastung:
- Bei Bergläufen wird die Muskulatur des Läufers häufig anders belastet als in der Ebene, insbesondere die Waden.
- Bergläufe erfordern i.d.R auch eine andere Ausrüstung (Schuhe, Rucksack) und sorgen so für zusätzliche Belastungen.
- Bergläufe finden häufig auf „schlechtem“ Untergründen statt (z.B. Geröll) die das Vorankommen beeinträchtigen und die Gelenke mehr belasten.
- Bei größerer Höhe wird die Luft merklich dünner, die Sauerstoffaufnahme sinkt und das erschwert den Lauf weiterhin.
- Jeder von uns weiß aus eigener Erfahrung – und nicht nur aus der Physik -, dass die Überwindung von Höhenmeter zusätzliche Kraft erfordert – und sei es nur eine Brücke mit kleinem Anstieg – und das vorankommen bei gleichem Einsatz langsamer ist.
Für das FSÄ wird i.d.R nur der letzte Punkt berücksichtigt, da die anderen derzeit quantitativ schlecht zugänglich sind bzw. nicht gemessen werden. Sie schlagen sich aber sehr wahrscheinlich in den messbaren Größen wie Herzfrequenz, Kadenz, Schrittweite, Standzeit und Vertikalhub nieder, wobei der quantitative Zusammenhang von Belastungsursache 1.-4. und Messergebnis hier nicht bekannt ist.
Der wichtige Zusammenhang zwischen Steigung und Laufarbeit ist in der folgenden Grafik dargestellt:
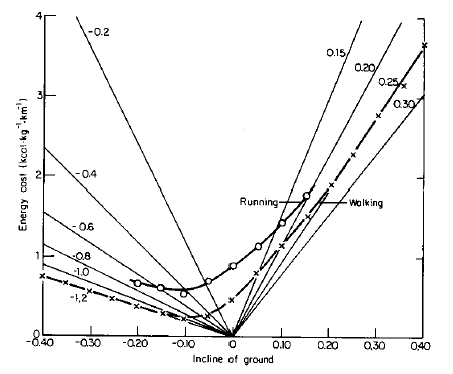
Quelle: McMahon (Muscles, Reflexes, and Locomotion. Princeton, NJ: Princeton University Press, 1984) zitiert nach „Dr. Lälles“
Die wesentlichen Linien sind hier die fürs Laufen und Gehen. Demnach steigt die erforderliche Arbeit mit der Steigung, sofern man nicht mehr als 10% Gefälle hat. Radfahrer sagen dazu gerne, dass man die gefahrene Höhe „fair“ zurück bekommt, sofern das Gefälle nicht zu groß ist. Dann nämlich verlässt man das Energieminimum und kann den Höhenverlust nicht optimal in Geschwindigkeit umsetzen.
Die Grafik zum Energieverbrauch mit den Linien für Laufen und Gehen kann man auch als Höhenlinien einer Funktion v=(Energy, gradient) auffassen. Wenn man den Berg schneller hinauf läuft, würde man eine weitere Linie oberhalb der „Running“ Linie erhalten. Wenn man langsamer hinauf läuft (läuft!), würde man eine Linie unterhalb der „Running“ Linie erhalten die evtl. die „Walking“ Linie schneidet, wenn das Tempo zu niedrig wird und ein Gangartwechsel effizienter ist (vgl. Beitrag zur Laufleistung in Watt). Das scheint bei längeren Läufen im profilierten Gelände z.B. Röntgenlauf oder Biel für die meisten von und Freizeitläufern ratsam zu sein.
Da wir hier die Arbeit oder Leistung nicht gemessen haben, nehmen wir als proxy Variable die Herzfrequenz (HF), vgl. Beitrag zur Laufleistung. Damit ist die Vermutung verbunden, dass x Herzschläge/min in der Ebene mit x Herzschlägen im profilierten Gelände Leistungsäquivalent sind. Wenn man die x Herzschläge in der Ebene für die Belastungszeit erbringen kann, dann sollte dies auch im profilierten Gelände möglich sein, wenn man Berge im Trainingsprogramm hat.
Die anderen durch Belastung und Steigung tangierten Messgrößen Kadenz, Standzeit und Vertikalhub werden zu einem Vektor y zusammengefasst und um den Einfluss von Herzfrequenz und Steigung bereinigt. Dies ist nötig, da sich sonst der Einfluss der Steigung auf das Tempo aufgrund Kolinearität nicht von den anderen Messungen trennen lässt. Für die Konstruktion der Funktion v=v(HF, Steigung | Kadenz, Standzeit, Vertikalhub) poolen wir Daten aus verschiedenen Läufen (einer Person, derzeit ca. 8300 Beobachtungen) und schätzen mit einem Regressionsansatz die Modelle
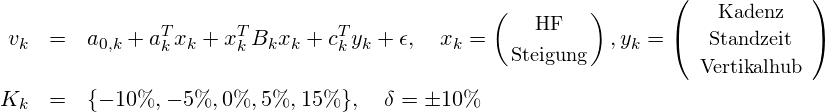
für unterschiedliche Steigungsklassen k. Die Steigungsklassen geben hier die nötige Flexibilität, den realen Verlauf gut zu approximieren und ermöglichen eine Asymmetrie in den Höhenlinien (≠ Ellipsoid mit 2 Hauptachsen), so dass die geschätzte Beziehung nur lokal quadratisch ist. Diese Lokalität wird im Regressionsansatz mit Gewichten ![]() für die Residuen nachgebildet.
für die Residuen nachgebildet.
Für die Geschwindigkeitsprognose zu einem Punkt (HF, Steigung) wird dann einfach eine gewichtete Linearkombination von ![]() der benachbarten Polynome ausgewertet.
der benachbarten Polynome ausgewertet.
Geschätzte Beziehung zwischen Geschwindigkeit, Steigung und Herzfrequenz beim Laufen
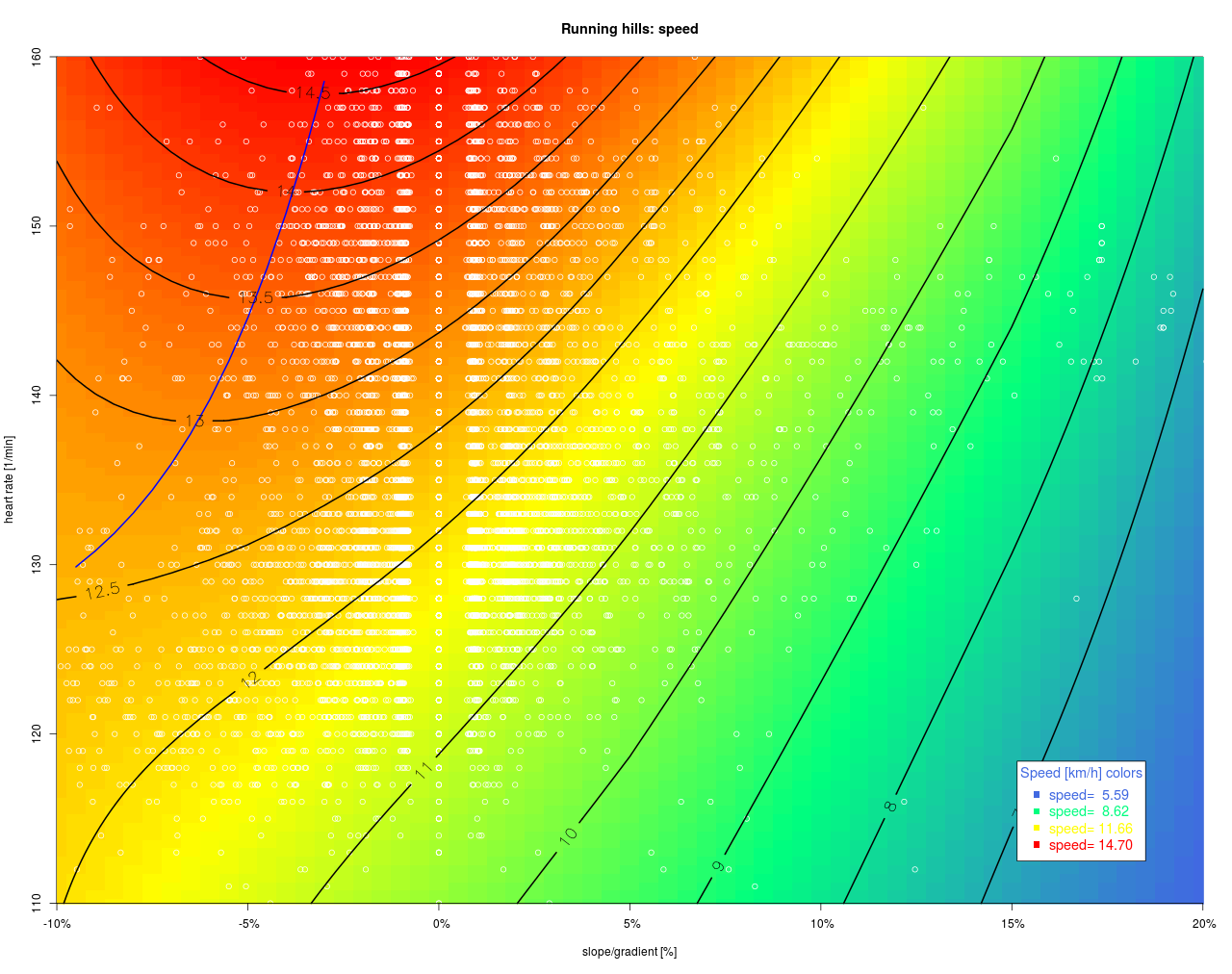
Bei einer Steigung von ca. 18% – 20% (das ist der Fähr-Rödel Anstieg an der Wupper in Leichlingen) wird bei einem Herzschlag von ca. 143 Schläge/min eine Geschwindigkeit von ca. 7.5 km/h erzielt. Das entspricht einem Vertikalaufstieg vom 1.350 m/Std und ist schon ziemlich sportlich, wenn man es mit Radfahrwerten vergleicht. Wenn man von diesem Punkt ausgehend bei gleicher Herzfrequenz Richtung 0% Steigung geht, nimmt die Geschwindigkeit zu. Bei 0% Steigung dürfte man dann ca. 13 km/h erreicht haben. In der Ebene würde man demnach 73,33% schneller laufen. Das Flachstreckenäquivalent zu einem Kilometer mit 18% Steigung ist somit 1,73 km.
Die blaue Linie markiert die Minimalpulswerte im Gefälle zu gegebener Geschwindigkeit. Darüber hinaus muss der Läufer seine Herzfrequenz steigern um das Tempo zu halten, obwohl das Gefälle zunimmt. Diese Grenze wird man deshalb nur ungern überschreiten.
Variantrechnungen zu Halbmarathon (HM) mit durchschnittlich 140 bpm Herzfrequenz
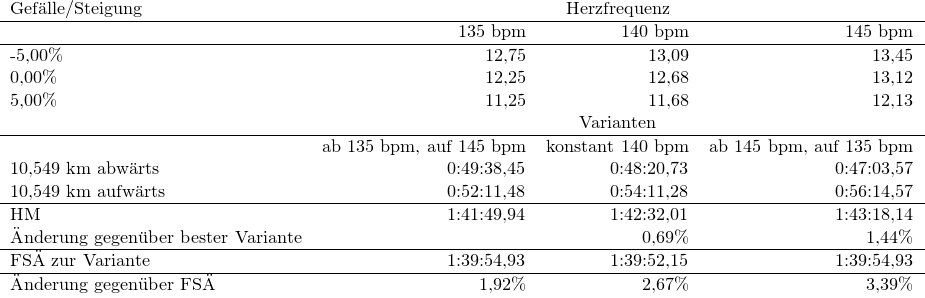
Die Flachstreckenzeit mit konstanten 140 bpm ist hier erwartungsgemäß am niedrigsten. Darauf folgt dann die 1. Variante mit langsamen Abstieg und schnellem Aufstieg. Konstante 140 bpm führen zu einer Verschlechterung von 0,69%. Und die Variante mit „Gas runter“ und bergauf langsamer schneidet am schlechtesten ab. Dort ist man dann auch beim „downhill“ jenseits der blauen Linie in der vorausgegangenen Grafik. Das FSÄ liegt ungefähr bei 1:40 und ist gegenüber der schlechtesten Variante um 3,4% besser.
Gegenüberstellung zur Naismith’s rule:
Hier wird davon ausgegangen das für zusätzliche 600 HM eine Stunde benötigt wird. Bei 13 km mit 18% Steigung kommt man auf 2.340 HM was zu einem Zuschlag von 13*0.18/0.6=3.9 Stunden führt. Für die 13 km werden jetzt 1+3.9 Stunden benötigt und die Geschwindigkeit beträgt somit 13/4.9=2.63 km/h. Wenn man jetzt abweichend den Naismith Zuschlag halbiert – laufen statt wandern – kommt man auf 4.41 km/h und damit noch weit unter den hier gemessenen Werten.
Anmerkung zu Daten, Verfahren und Anwendung:
- Die Karte beruht auf individuellen Laufdaten und reflektiert das Leistungsniveau eines Athleten, ist also nicht ohne weiteres auf andere Läufer übertragbar. Insbesondere dürfte das Gewicht des Sportlers Einfluss auf den Abstand der Isogeschwindigkeitslinien haben. Vermutlich liegen diese bei leichteren Läufern enger zusammen und bei Schwereren weiter auseinander.
- Die zugrunde liegenden Messwerte sind als weiße Punkte dargestellt. Regionen der Karte, in denen kaum Punkte liegen, dürften mit großen Vertrauensbereichen (=Unsicherheit) abgebildet sein. Man sieht hier, dass dieser Läufer überwiegend im Flachen läuft und würde deshalb schon zu gemäßigtem Pace am Berg raten.
- Schaut man sich die Region um das Geschwindigkeitsmaximum an, so sind die Höhenlinien nicht symmetrisch um die 0% Steigungsachse, sondern leicht nach links „ausgebeult/verschoben“. Das entspricht auch den Erwartungen und man sollte in diesem Bereich („Mit Vollgas den Berg herunter“) testweise mehr Daten sammeln, auch wenn das langfristig für Knie und Fuß ungünstig seien könnte.
- Ebenso wäre es interessant, den Berg mal langsamer mit niedriger Herzfrequenz hoch zu laufen. Damit könnte man die Herzfrequenzabhängigkeit des FSÄ abschätzen. Es stellt sich die Frage, ob der Geschwindigkeitsertrag einer gesteigerten Herzfrequenz überall der gleiche ist. Nach diesen Berechnungen, liegt der Ertrag im mittleren Bereich am niedrigsten d.h. die Höhenlinien sind weit auseinander. Das kann aber auch auf die dünne Datenbasis an den Rändern zurück zuführen sein.
- Wie bereits vorher erwähnt, kann es bei steilen Passagen sinnvoller sein, einen Gangartwechsel vorzunehmen d.h. zu gehen. Das ist hier nicht abgebildet. Vermutlich ist dies ab ca. 6-7 km/h die bessere Wahl.
- Man könnte versuchen, den Steigungsinduzierten Geschwindigkeitsverlust bei gleicher Herzfrequenz in Leistung d.h. Watt umzurechnen.
Wie berechnet man nun das FSÄ für einen ganzen Lauf? Am besten nicht zu Fuß und per Hand!
- Hat man den profilierten Lauf mit Herzfrequenz und Geschwindigkeit vorliegen, schaut man für jedes Segment in der Funktion v=v(HF, Steigung) den Wert v=v(HF, Steigung=0) nach und berechnet den Aufschlag fürs Gelände. Hier kann es eventuell günstig sein, einen Korrekturfaktor c aus der Funktion v(HF, Steigung) und der beobachteten Geschwindigkeit v zu berücksichtigen und c*v(HF, Steigung=0) anzusetzen. Letztlich hängt dies mit der Frage zusammen, welchen Daten man mehr Vertrauen schenkt: der ermittelten Karte oder dem aufgezeichneten Track (Länge, Höhe) mit Herzfrequenz (vgl. die diskutierten Fehlerquellen bei der Messung).
- Hat man nur den GPS-Track ohne HF vorliegen, muss man für die HF eine realistische Annahme machen z.B HF=Mittelwert und ermittelt den Wert v=v(HF=Mittelwert, Steigung=0) und daraus den Aufschlag.
- Bei diesen Berechnungen sollte man das Höhenprofil des Laufs anschauen und offensichtliche Ausreißer oder häufiges Auf und Ab (Rauschen) durch geeignete Methoden zuvor entfernen.
Continued: „Fähr-Rödel“
Für den Eingangs dargestellten Lauf wird nun das Flachstreckentempo und das Flachstreckenäquivalent berechnet. Dazu wird zunächst ein Korrekturfaktor c mit
![Rendered by QuickLaTeX.com \[ c = \frac{\bar{v}}{\bar{\hat{v}}}, \quad \bar{v}= \frac{ \sum_i \mbox{\small distance}_i}{\sum_i t_i}, \quad \bar{\hat{v}} = 1/N \sum_i^N v(\mbox{\small HF}_i, \mbox{\small Steigung}_i) \]](http://lt-pappelallee.de/wp-content/ql-cache/quicklatex.com-1095f149f52780055e1fd9347bc85da2_l3.png)
berechnet. ![]() ist dann die geschätzte Geschwindigkeit zu gegebener Herzfrequenz (i) und Steigung (i) die im Mittel mit den Daten der Laufuhr übereinstimmt. Für das Flachstreckenäquivalent müssen jetzt nur noch die Werte
ist dann die geschätzte Geschwindigkeit zu gegebener Herzfrequenz (i) und Steigung (i) die im Mittel mit den Daten der Laufuhr übereinstimmt. Für das Flachstreckenäquivalent müssen jetzt nur noch die Werte ![]() berechnet werden. Diese sind in der folgenden Grafik dargestellt.
berechnet werden. Diese sind in der folgenden Grafik dargestellt.
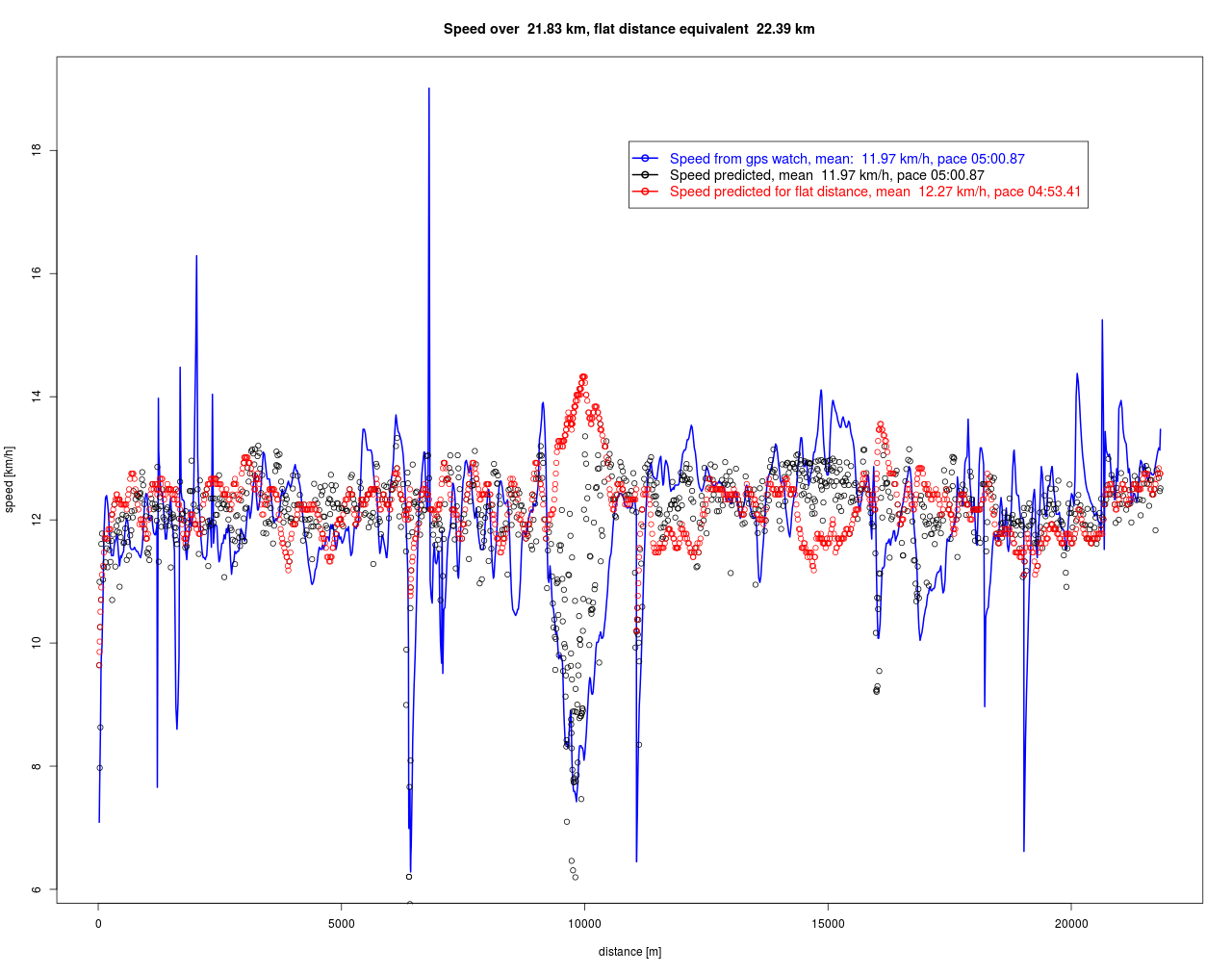
Das FSÄ ist hier 560 m länger als der zurückgelegte Weg, was erstaunlich wenig ist, angesichts der „Quälerei“ am Aufstieg „Fähr-Rödel“ mit ca. 20% Steigung. Immerhin wird diese mit über 14 km/h honoriert. Aber es gibt eben auch Abzüge für die Gefällestücke, die man hätte schneller laufen können. Im Flachen wäre man auf dieser Strecke deshalb nur 2.5% schneller gewesen. Beide geschätzte Zeitreihen zeigen eine deutlich niedrigere Streuung in der Geschwindigkeit als die Messungen der Laufuhr, was positiv zu bewerten ist, da die „spikes“ sehr wahrscheinlich Ausreißer sind.
Dieser Lauf wurde auch nach strava hochgeladen und wird dort mit einem mittlerem Tempo 5:01 und einem SAT-Tempo (das dürfte dem Flachstreckenäquivalent entsprechen) von 4:56 ausgewiesen. Die Höhe hat also bei strava zu einem Abzug von 5 Sekunden/km geführt, während dieses Modell zu einem Abzug von 7,46 Sekunden/km führt. Damit fällt die Honorierung der Höhenleistung noch schwächer aus und daran darf gezweifelt werden. Umgekehrt bedeutet dies, dass die Zuschläge für Höhenmeter wahrscheinlich zu gering sind und dies kann zu unangenehmen Fehleinschätzungen bei Bergläufen führen. Hier würde man aus Risikogründen schon lieber größere Werte ansetzen.
Am besten man probiert es einfach mal selber aus: Also Laufsachen anziehen und den nächsten Hügel in der Umgebung angehen. Dazu dann einen Lauf ähnlicher Länge und mit ähnlicher Herzfrequenz laufen und diese beiden Zeitreihen gegenüberstellen.
