Absprungwinkel
Contents
Für die Herleitung der Laufleistung in Watt war der Absprungwinkel von Bedeutung. Neben Schrittfrequenz und Kadenz sind die Winkel beim Laufen ein in jüngster Zeit stark diskutiertes Thema, vgl. Julian Reus aber auch Chris Solinsky.
Die Angaben zum Vertikalhub im Video mal kurz nachgerechnet
strides: 6200 / 10.000 m; vertical oscillation: 15,24 cm (sehr groß) daraus folgt:
total climb = 945 HM (das deckt sich mit den Angaben im video)
stride length = 1,61 m (das ist schon sehr groß, zumindest für uns Freizeitläufer)
Bestzeit von Chris Solinsky ist 27 min / 10.000m. Wenn man diese Zeit dem Lauf im Video zugrundelegt folgt daraus:
Kadenz = 230 strides/min :Das ist wieder sehr groß, und unverträglich mit den Angaben in runnersworld für Eliteläufer. Selbst wenn man mit 30min/10.000m rechnet kommt man auf 206 Schritte/min. Erst bei 32 min /10.000m kommt man auf eine Schrittfrequenz von 190 Schritte/min die man nach runnersworld bei Topläufern erwarten kann.
Mit zunehmender Digitalisierung (Sensoren) können immer präzisere Aussagen zur Lauftechnik gemacht werden und darauf aufbauend Optimierungen erfolgen. Sensoren, Biomechanik, quantitative Modelle und genügend Rechenpower sind wahrscheinlich heute für einen großen Teil der Erfolge verantwortlich und haben Expertenurteile zumindest in Teilen schon ersetzt. Und letztlich kann man dann auch das Laufen Maschinen überlassen.
Nach Heise ist der Laufrobotor „cheetah“ mit 45km/h derzeit schon schneller als Usain Bolt. Sehr wahrscheinlich wird die erforderliche Rechenleistung für solche Laufroboter die Anforderungen der Apollo Mondlandung bei weitem übertreffen (vgl. Zeit). Klassische Mechanik kann selbst heute zu einer Herausforderung für Computer werden.
Es ist natürlich nicht unser Ziel, das Laufen Maschinen zu überlassen, denn wir wollen uns selbst bewegen. Für diese komplexen Modelle ist viel Forschung, Gerät und IT-Technik Voraussetzung die für uns Freizeitläufer derzeit unerschwinglich ist. Aber wir werden von der Forschung profitieren und es gibt ja schon im low budget Bereich highspeed Kameras und Analysewerkzeuge, mit denen man den Lauf detaillierter betrachten kann. Die Video’s zeigen, in welche Richtung die Entwicklung geht und wahrscheinlich werden die nächsten Jahre viel Neues für uns Läufer bringen.
Im Folgenden wird einfacher verfahren und auf den Daten einer Laufuhr – für Freizeitläufer – mit den Feldern Zeit, Kadenz, Geschwindigkeit und Vertikalhub aufgesetzt.
Physikalisches Modell: Wurfparabel
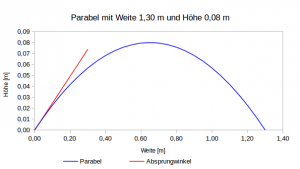
Die Flugbahn beim Wurf kann mit folgendem einfachen Modell (vgl. Wurfparabel) beschrieben werden.
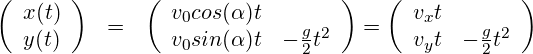
x(t) : horizontale Koordinate in Abhängigkeit der Zeit t
y(t) : vertikale Koordinate in Abhängigkeit der Zeit t
α : Absprungwinkel
![]() : Geschwindigkeit beim Absprung in Richtung α
: Geschwindigkeit beim Absprung in Richtung α
d.h.
- in Richtung
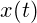 gleichförmige und ungebremste Bewegung mit der horizontlen Komponente von
gleichförmige und ungebremste Bewegung mit der horizontlen Komponente von 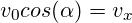 ,
, - in Richtung
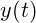 durch Schwerkraft
durch Schwerkraft 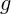 gebremste Bewegung
gebremste Bewegung 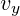 .
.
Absprungwinkel aus Scheitelpunkt der Wurfparabel
Ableitung des Absprungwinkels aus den Scheitelpunkt ![]() der Wurfparabel
der Wurfparabel
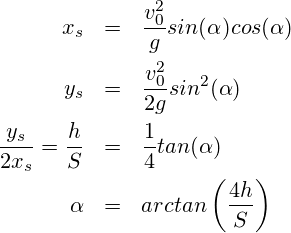
Wenn man nach dieser Gleichung den Absprungwinkel ![]() berechnet und dann über eine weiter Gleichung
berechnet und dann über eine weiter Gleichung ![]() z.B.
z.B. ![]() bestimmt hat man sämtliche Parameter zur Parabel festgelegt. Wendet man dies nun auf mit einer Laufuhr gemessene Werte an, stellt man i.d.R. fest, dass die unberücksichtigt geblieben Gleichungen nicht erfüllt werden d.h. man hat Fehler in den Gleichungen zu
bestimmt hat man sämtliche Parameter zur Parabel festgelegt. Wendet man dies nun auf mit einer Laufuhr gemessene Werte an, stellt man i.d.R. fest, dass die unberücksichtigt geblieben Gleichungen nicht erfüllt werden d.h. man hat Fehler in den Gleichungen zu ![]() . Dies kann einerseits daran liegen, dass das Modell zu einfach und damit falsch ist, andererseits könnten Messfehler das Bild trüben. Aus den Beitrag zur Höhe wissen wir, dass die per gps-Uhr gemessene Geschwindigkeit fast nie mit dem Quotient aus Länge und Zeit übereinstimmt, weil
. Dies kann einerseits daran liegen, dass das Modell zu einfach und damit falsch ist, andererseits könnten Messfehler das Bild trüben. Aus den Beitrag zur Höhe wissen wir, dass die per gps-Uhr gemessene Geschwindigkeit fast nie mit dem Quotient aus Länge und Zeit übereinstimmt, weil ![]() z.B. über einen Kalman Filter ermittelt wird. Deshalb wird im Folgenden versucht die Fehler auszugleichen.
z.B. über einen Kalman Filter ermittelt wird. Deshalb wird im Folgenden versucht die Fehler auszugleichen.
Parameterschätzung
Mit dem physikalische Modell können die gemessenen Werte der Laufuhr ![]() i.d.R nicht gleichzeitig exakt getroffen werden. Man kann aber versuchen eine Annäherung dazu mit folgender Parameterschätzung zu
i.d.R nicht gleichzeitig exakt getroffen werden. Man kann aber versuchen eine Annäherung dazu mit folgender Parameterschätzung zu ![]() im Rahmen eines nichlinearen Modells zu bestimmen.
im Rahmen eines nichlinearen Modells zu bestimmen.
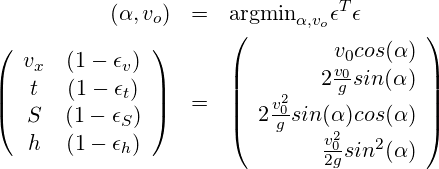
wobei
![]() : die per gps gemessene Geschwindigkeit [m/s]
: die per gps gemessene Geschwindigkeit [m/s]
![]() : die Zeit pro Schritt aus
: die Zeit pro Schritt aus ![]() Kadenz abgeleitet [s]
Kadenz abgeleitet [s]
![]() : die Schrittweite [m] aus
: die Schrittweite [m] aus ![]() abgeleitet
abgeleitet
![]() : der vertikale Hub [m] nach Garmin HRM Messung
: der vertikale Hub [m] nach Garmin HRM Messung
In diesem Modell werden die relativen Fehler minimiert. Da jeder einzelne Fehler in einem anderen nichlinearen Zusammenhang mit den unbekannten Parametern steht, kann dies nicht mit standardmodellen zur nichtlinearen Regression erfolgen, sondern muss mit allgemeiner nichtlinearer Optimierung gelöst werden. Dazu wird ein CG-Verfahren implementiert. Als Startpunkt kann man hier die Lösungen zu zwei der 4 Gleichungen wählen.
![Rendered by QuickLaTeX.com \[\begin{array}{lrrr} & \mbox{observed values} & \mbox{commercial Solver} & \mbox{CG Verfahren} \\ \hline $v & 3.4150 & 3.7736 & 3.4675 \\ t & 0.3704 & 0.2903 & 0.2735 \\ x & 1.2648 & 1.0954 & 0.9482 \\ y & 0.0917 & 0.1033 & 0.0917 \\ \hline \hat{\alpha} & & 20.67145 & 21.14802 \\ \hat{v}_0 & & 4.0332 & 3.71786 \\ \hline e_v & & 0.3586 & 0.0525 \\ e_t & & -0.0801 & -0.0969 \\ e_x & & -0.1695 & -0.3166 \\ e_y & & 0.0116 & 0.0000 \\ \hline e_v \% & & 10.50\% & 1.54\% \\ e_t \% & & 21.63\% & 26.17\% \\ e_x \% & & 13.40\% & 25.03\% \\ e_y \% & & 12.67\% & 0.00\% \\ \hline \hline \mbox{objective} & & 14.5491\% & 13.1833\% \\ \end{array}\]](http://lt-pappelallee.de/wp-content/ql-cache/quicklatex.com-c546e98c1eaf897ae7d1883337a6612d_l3.png)
Die Ergebnisse aus der Tabelle zeigen, dass selbst dieses kleine Problem je nach Algorithmus zu unterschiedlichen Lösungen führen kann. Relativ stabil ![]() wird aber der Absprungwinkel mit ca 21. Grad geschätzt. Unbefriedigend sind hingegen die Anpassungen an t und x und die damit assoziierte Kadenz und Schrittweite.
wird aber der Absprungwinkel mit ca 21. Grad geschätzt. Unbefriedigend sind hingegen die Anpassungen an t und x und die damit assoziierte Kadenz und Schrittweite.
Mathematisches Modell
In diesem Abschnitt soll die Flugbahn des Läufers ohne physikalische Ableitungen bestimmt werden. Zur Approximation wählen wir eine einfache Parabel sowie 2 Parabeln, die sich in ihren Scheitelpunkten treffen.
Ableitung des Absprungwinkels aus einer Parabel durch die Punkte ![]()
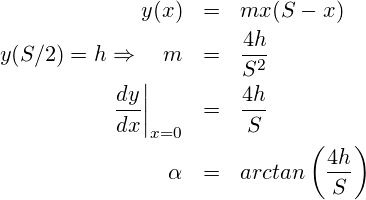
Für die einfache Parabel kommen wir erwartungsgemäß zum selben Ergebnis des physikalischen Modells. Nun ist diese Funktionsform aber weniger flexible wie die der zusammengesetzten Parabeln.
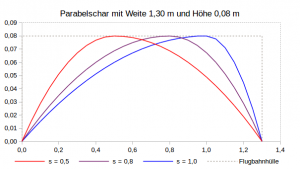
- Es wird eine symmetrische Flugbahn links und rechts vom Scheitelpunkt unterstellt.
- Da die Wurfparabel in der horizontalen eine ungebremste Bewegung unterstellt und somit Luftwiderstand nicht abbildet, kann die reale Flugbahn von der theoretischen deutlich abweichen. Die Ableitungen zur Flugbahn eines Fussballs (vgl. Prof. Metin Tolan) haben zu folgenden Schlüssen geführt:
1) Diese Abweichung wird tendenziell Größer, je höher die Anfangsgeschwindigkeit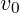 und Querschnittfläche
und Querschnittfläche 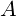 und desto niedriger die Masse des bewegten Körpers ist.
und desto niedriger die Masse des bewegten Körpers ist.
2) Die Flugbahnen sind nicht mehr symmetrisch zum Scheitelpunkt. Sie steigen anfangs flacher an und fallen gegen Ende stärker ab.
3) Die komplexen Gleichungen für Stokes und Newton-Reibung sind wahrscheinlich für das Laufproblem „überzogen“. - Die optimalen Abwurfwinkel in der Leichtathletik (Speer, Hammer, Kugel, Diskus) liegt deutlich unter den optimalen 45 Grad, die sich bei Gültigkeit der einfachen Wurfparabel ergeben würden. Deshalb dürfte die Flugbahn mit zusammengesetzten Parabeln eine bessere Approximation sein. Für Läufer dürften diese Effekte eher eine untergeordnete Bedeutung haben. Für zwei zusammengesetzte Parabeln mit vorgegebener Schrittweite S, Höhe h und Scheitelpunkt
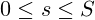 mit Form
mit Form 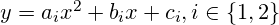 ergeben sich die Parameter
ergeben sich die Parameter
![Rendered by QuickLaTeX.com \[\begin{array}{lccc} & a & b & c \\ \hline \mbox{Parabel 1} & -\frac{h}{s^2} & \frac{2h}{s} & 0\\ \mbox{Parabel 2} & -\frac{h}{(S-s)^2} & \frac{2hs}{(S-s)^2} & \ldots \end{array} \]](http://lt-pappelallee.de/wp-content/ql-cache/quicklatex.com-73fc7393a5e7fdf48e3a555d1836ce83_l3.png)
Der Absprungwinkel ergibt sich hier aus der ersten Parabel mit
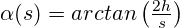 und liefert für
und liefert für 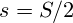 natürlich den Wert der Wurfparabel. Für realistische Flugbahnen dürfen aber eher Werte
natürlich den Wert der Wurfparabel. Für realistische Flugbahnen dürfen aber eher Werte 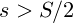 relevant sein die zu einem kleineren Absprungwinkel führen. Unterstellt man bei einem Lauf ein konstantes Verhältnis von
relevant sein die zu einem kleineren Absprungwinkel führen. Unterstellt man bei einem Lauf ein konstantes Verhältnis von 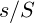 so sind die berechneten Steigungen des zusammengesetzten Modells und des Wurfparabelmodells proportional. Bis auf einen – hier leider unbekannten – positiven Skalierungsfakor ändert sich nichts, und wir können dennoch Richtungsaussagen machen.Unter Verwendung der Definitionsgleichung für die Schrittlänge
so sind die berechneten Steigungen des zusammengesetzten Modells und des Wurfparabelmodells proportional. Bis auf einen – hier leider unbekannten – positiven Skalierungsfakor ändert sich nichts, und wir können dennoch Richtungsaussagen machen.Unter Verwendung der Definitionsgleichung für die Schrittlänge 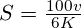 und dem Absprungwinkel der Wurfparabel erhält man
und dem Absprungwinkel der Wurfparabel erhält man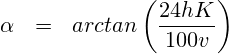
Die arctan(x) Funktion ist im relevanten Laufbereich nahezu linear, vgl. folgende Abbildung.
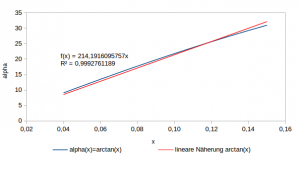
Mit der linearen Näherung zu arctan(x) kann man α mit
![Rendered by QuickLaTeX.com \begin{eqnarray*} \alpha & \approx & c \frac{h K}{v} \\ v \alpha & \approx & c \underbrace{h \,\, K}_{\mbox{Hubleistung [m/min]}} \end{eqnarray*}](http://lt-pappelallee.de/wp-content/ql-cache/quicklatex.com-6f5e8b0c24a4c1346ef927dbee220ca4_l3.png)
gut approximieren, wobei c eine positive Konstante ist. Die erbrachte Hubleistung des Läufers wird hier auf das Produkt von Geschwindigkeit und Absprungwinkel verteilt. Wird eine hohe Geschwindigkeit bei gegebener Leistung angestrebt ist ein kleiner Absprungwinkel förderlich. Diesen kann der Läufer beeinflussen:
- Den Absprungpunkt möglichst weit hinter den Körperschwerpunkt legen.
- Dies ist i.d.R besser möglich, wenn das Absprungbein lang gemacht wird in dem das Knie beim Absprung vollständig durchgestreckt wird.
Gegenüberstellung ungünstiger und günstiger Absprungwinkel für das Lauftempo
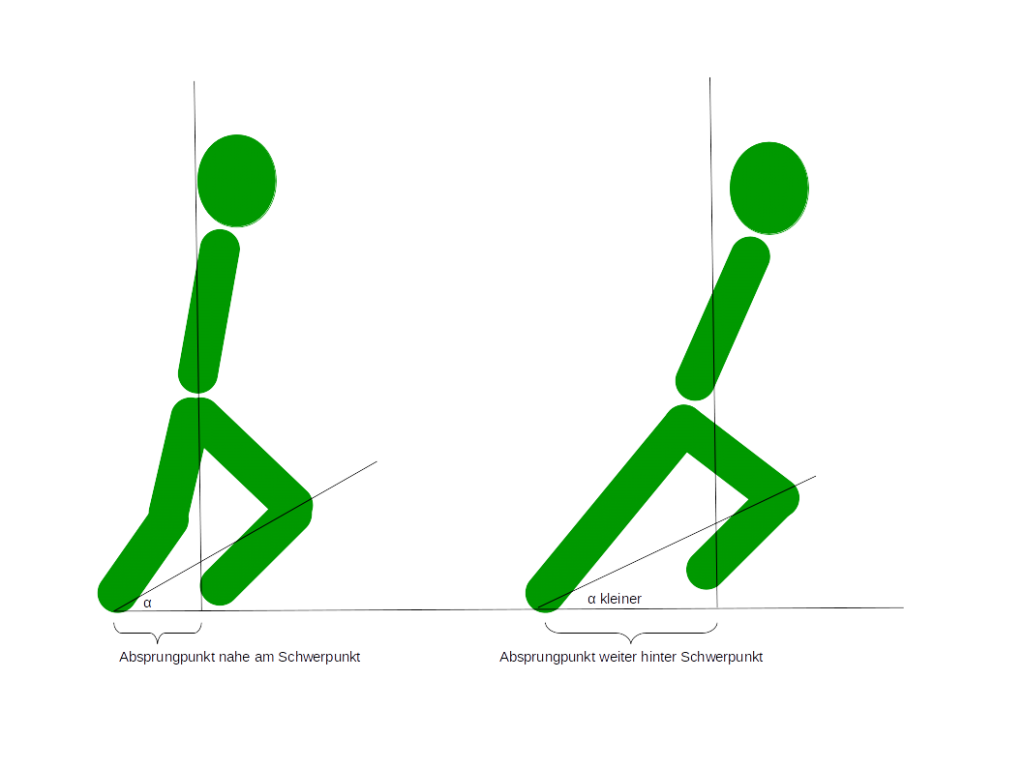
Daraus resultieren dann häufig – nach Erfahrung des Autors –
- eine stärker nach vorn geneigte Haltung des Oberkörpers
- eine höhere Schrittfrequenz (Kadenz k), die wiederum die Aufstiegsleistung erhöht
